پکیج SciPy (بخوانید سای پای)  یک پکیج علمی و اوپن سورس مبتنی بر زبان پایتون است و برای انجام محاسبات علمی و مهندسی مورد استفاده قرار می‌گیرد. کتابخانه‌ی SciPy بر مبنای کتابخانه‌ی NumPy است و امکان کار با آرایه‌های n بُعدی را فراهم می‌کند. این کتابخانه برای کار با آرایه‌های Numpy ایجاد شده است و بسیاری از عملیات محاسباتی و بهینه‌سازی را به طور کارا ممکن می‌کند. هر دو پکیج Numpy و Scipy روی سیستم عامل‌های موجود کار می‌کنند و به راحتی نصب می‌شوند. در این مقاله به آموزش کتابخانه‌ی SciPy در پایتون خواهیم پرداخت و در پایان شما متوجه خواهید شد که SciPy چیست و می‌توانید پروژه‌ی خود را به کمک scipy شروع کرده و پیش ببرید.

Sub-packageهای SciPy چیست

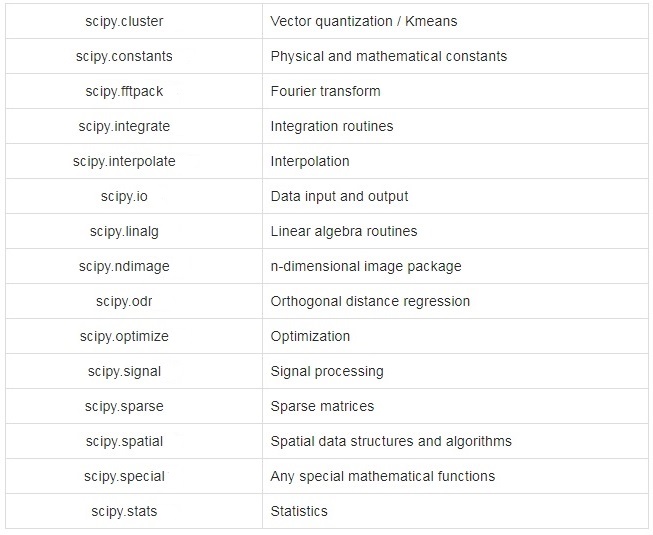
SciPy زیر پکیج‌هایی دارد که هرکدام به منظور پوشش اعمال محاسباتی در زمینه‌ی خاصی توسعه یافته‌اند. این زیرپکیج‌ها در جدول زیر با توضیح مختصری از کارکرد آن‌ها آمده‌ است.

ساختارداده‌های SciPy چیست

ساختار داده‌ی پایه‌ای که در SciPy مورد استفاده قرار گرفته آرایه‌های چند بُعدی در NumPy است. NumPy برخی توابع را برای کار با جبرخطی، تبدیل فوریه و تولید اعداد تصادفی فراهم کرده‌است. اما این توابع به گستردگی توابع ارائه شده‌ی متناظر در پکیج SciPy نیست.

نصب SciPy

یکی از روش‌های معمول  نصب Scipy استفاده از دستور زیر است.

pip install pandas

اگر ما از توزیع پکیج آناکوندا استفاده کنیم، Scipy به طور پیش‌فرض در آن نصب شده است. برای یادگیری نصب آناکوندا می‌توانید به مقاله‌ی آموزش کتابخانه NumPY مراجعه کنید.

توابع پایه‌ای در SciPy چیست

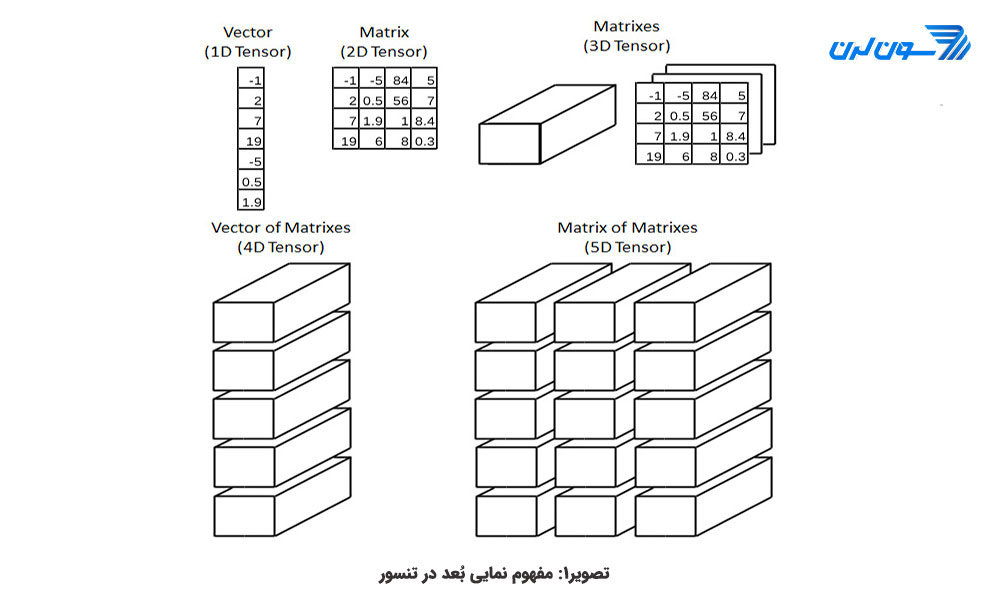
به طور کلی توابع NumPy در پکیج Scipy موجود است و نیازی به وارد کردن کتابخانه‌ی NumPy نیست. از مهم‌ترین توابع موجود در numpy آرایه‌های چند بعدی یک‌دست است. این آرایه‌ها مشابه جدولی از اجزائی (عموماً عدد) است که همگی نوع یکسان دارند و اندیس‌های عددی صحیح و مثبت دارند.

در Numpy  به ابعاد داده محور (axes) گفته می‌شود و تعداد محورها مرتبه‌ی آرایه یا rank نامیده می‌شود. در ادامه بردارها و ماتریس‌های عددی در NumPy را به صورت سریع و کلی مرور می‌کنیم. از آنجایی که Scipy روی Numpy بنا شده، یادآوری این مطالب ضروری است.

بردارها در NumPy

یک بردار در NumPy می‌تواند به چند طریق مختلف ایجاد شود. برخی از این روش‌ها در زیر آمده است:

تبدیل لیست پایتون به آرایه

مثال زیر را در نظر بگیرید:

import numpy as np
list = [1,2,3,4]
arr = np.array(list)
print (arr)

خروجی کد بالا به شکل زیر است:

[1 2 3 4]

در Numpy توابع داخلی برای ایجاد آرایه‌ها ساخته شده است. برخی از این توابع در زیر توضیح داده شده است.

ماتریس صفر

تابع zeros به شکل zeros(shape) آرایه‌ای است که با مقادیر صفر به تعداد shape تعریف شده، پر شده است. نوع پیش‌فرض float64 بیتی است. مثال زیر را در نظر بگیرید:

import numpy as np
print np.zeros((2, 3))

خروجی کد بالا آرایه‌ای به شکل زیر است:

array([[ 0., 0., 0.], [ 0., 0., 0.]])

ماتریس یک

تابع ones(shape) آرایه‌ای با مقادیر یک به تعداد shape ایجاد می‌کند و مشابه zeros است. مثال زیر را در نظر بگیرید:

import numpy as np
print np.ones((2, 3))

خروجی به شکل زیر است:

array([[ 1., 1., 1.], [ 1., 1., 1.]])

تابع arange

تابع arange لیستی از اعداد تولید می‌کند که آن مقادیر به طور صعودی مرتب‌ هستند. مثال زیر را در نظر بگیرید:

import numpy as np
print np.arange(7)

خروجی به شکل زیر است:

array([0, 1, 2, 3, 4, 5, 6])

تعیین نوع مقادیر

مثال زیر را در نظر بگیرید:

import numpy as np
arr = np.arange(2, 10, dtype = np.float)
print arr
print ("Array Data Type :",arr.dtype)

خروجی کد شامل آرایه‌ای با مقادیر مرتب صعودی است که از عدد 2 شروع می‌شود و نوع مقادیر به اعشاری 64 بیتی تغییر یافته است.

[ 2. 3. 4. 5. 6. 7. 8. 9.] Array Data Type : float64

ماتریس

یک ماتریس آرایه‌ای دوبعدی است که در طی انجام انواع عملیات ماهیت دو بعدی خود را حفظ می‌کند. نحوه‌ی تعریف ماتریس به شکل زیر است:

import numpy as np
print np.matrix('1 2; 3 4')

خروجی، ماتریسی به شکل زیر است:

matrix([[1, 2], [3, 4]])

به شکل زیر نیز می‌توان ترانهاده‌ی ماتریس را محاسبه کرد:

import numpy as np
mat = np.matrix('1 2; 3 4')
print (mat.H)

که خروجی به شکل زیر است:

matrix([[1, 3],        [2, 4]])

خوشه‌بندی یا Clustering در SciPy

خوشه‌بندی K-means روشی برای یافتن خوشه‌ها و مراکز آن‌ها در یک مجموعه داده‌ی بدون برچسب است. خوشه‌ها مجموعه‌ای از نقاط داده‌ای هستند که مشابه همدیگرند و فاصله‌ی میان آن نقطه داده‌ها با همدیگر کمتر از سایر خوشه هست. با K مرکز خوشه‌ای داده شده، الگوریتم K-means دو مرحله‌ی زیر را تکرار می‌کند

• برای هر مرکز، زیرمجموعه‌ای از نقاط آموزشی که به آن مرکز، نسبت به سایر مراکز نزدیک‌ترند، انتخاب می‌شوند.

• میانگین مقدار هر ویژگی برای هر مرکز، براساس مقادیر نقاط داده برای آن ویژگی محاسبه می‌شود و بردار حاصل از میانگین ویژگی‌ها در هر خوشه، به عنوان مرکز جدید خوشه‌ای در نظر گرفته می‌شود.

این دو مرحله تا زمانی که مقادیر مراکز خوشه تغییر چندانی نکند، تکرار می‌شوند. در نهایت هر نمونه داده‌ی جدید مانند x، به خوشه‌ی مشابه‌اش تعلق می‌گیرد.

اجرای K-means با SciPy

کتابخانه‌ی SciPy امکان اجرای بهینه‌ی الگوریتم k-means را با پکیج خوشه‌بندی فراهم می‌کند. وارد کردن K-means نحوه‌ی وارد کردن و استفاده از تابع k-means به شکل زیر است:

from SciPy.cluster.vq import kmeans,vq,whiten

تولید داده برای اجرای خوشه‌بندی، به داده‌هایی نیاز داریم. می‌توانیم این داده‌ها را به شکل زیر ایجاد کنیم:

from numpy import vstack,array
from numpy.random import rand
# data generation with three features
data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))

کد بالا داده‌هایی به شکل زیر تولید می‌کند:

array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],       [ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],       [ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],       …………….

در خوشه‌بندی به کمک Kmeans بهتر است داده‌های مربوط به هر ویژگی را نرمال‌سازی کنیم. داده‌ها اگر در مقیاس مشابهی باشند و پراکندگی یکسانی داشته باشند، خوشه‌بندی کاراتر است.

پاک‌سازی داده برای این‌کار کد زیر را اجرا می‌کنیم:

# whitening of data
data = whiten(data)

محاسبه‌ی kmeans با سه خوشه

برای تقسیم داده‌ها به سه خوشه کد زیر را اجرا می‌کنیم:

# computing K-Means with K = 3 (3 clusters)
centroids,_ = kmeans(data,3)

کد بالا الگوریتم kmeans را روی مجموعه داده‌ها اجرا کرده و سه خوشه تولید می‌کند. الگوریتم kmeans مراکز خوشه‌ها را تا زمان رسیدن به مقدار مناسب محاسبه می‌کند. تغییر مقادیر خوشه‌ها تا مرحله‌ای تکرار می‌شود که تفاوت مقدار خوشه در آن مرحله با مرحله‌ی قبلی‌اش از یک مقدار آستانه کمتر باشد. می‌توانیم مقدار مراکز خوشه‌ها را که در متغیر centroids قرار داده شده است را به کمک کد زیر به دست آوریم:

print(centroids)

مراکز سه خوشه‌ی بالا سه بردار زیر است که هر بردار سه مقدار دارد که همان تعداد ویژگی‌های داده‌های ما هستند.

print(centroids)[ [ 2.26034702  1.43924335  1.3697022 ]                  [ 2.63788572  2.81446462  2.85163854]                  [ 0.73507256  1.30801855  1.44477558] ]

هر داده‌ی جدید را می‌توان با کد زیر به خوشه‌ی مناسبش، اختصاص داد.

# assign each sample to a cluster
clx,_ = vq(data,centroids)

تابع vq هر بردار داده را با مراکز خوشه‌ها مقایسه می‌کند و به نزدیک‌ترین خوشه اختصاص می‌دهد. این تابع خوشه‌ای را که داده به آن تعلق می‌گیرد را، برمی‌گرداند. با دستور زیر می‌توانیم چگونگی خوشه‌بندی داده‌ها و اینکه متعلق به کدام یک از سه خوشه‌ی 0، 1 یا 2 هستند را ببینیم.

# check clusters of observation
print (clx)

خروجی کد بالا به شکل زیر است:

array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1,  0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0, 2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)

مقادیر ثابت در SciPy چیست

پکیج scipy.constant مقادیر ثابت متعددی را می‌تواند تولید کند. باید مقدار ثابت درخواستی را با دستور import وارد کنیم و سپس از آن استفاده کنیم. برای مثال عدد پی (Pi) را به شکل زیر استفاده می‌کنیم:

#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)

خروجی کد بالا برای هر دو کتابخانه‌ی scipy و math به شکل زیر است:

sciPy - pi = 3.1415926535897931 math - pi = 3.1415926535897931

لیست مقادیر ثابت موجود

مقادیر ثابت فراوانی در ریاضیات و فیزیک وجود دارد. همچنین اختصارات زیادی وجود دارد که همیشه معنی یکسانی را می‌رساند. به طور مثال واحدهای تعریف شده برای جرم و طول را با kg و inch نشان می‌دهند. به خاطر سپاری اختصارات مربوط به مقادیر ثابت کار سختی است. برای اینکه اطلاعات بیشتر در این زمینه کسب کنید و بدانید که اختصارات و علائم تعریف شده در SciPy چیست، به document آن مراجع کنید. راه حل آسان برای فهمیدن اینکه هر کلمه‌ی کلیدی در SciPy چیست و به چه مقدار ثابتی اختصاص یافته است، به کارگیری متد scipy.constant.find() است. به مثال زیر توجه کنید:

import scipy.constants
res = scipy.constants.physical_constants["alpha particle mass"]
print (res)

برنامه‌ی بالا خروجی زیر را تولید می‌کند که لیستی از کلیدهای منطبق با کلید مورد جستجوی ماست.

[   'alpha particle mass',   'alpha particle mass energy equivalent',   'alpha particle mass energy equivalent in MeV',   'alpha particle mass in u',   'electron to alpha particle mass ratio' ]

تبدیل فوریه: FFTPack در SciPy چیست

تبدیل فوریه محاسباتی به منظور تبدیل تابع از دامنه‌ی زمانی به دامنه‌ی فرکانسی است و رفتار تابع را در حوزه‌ی فرکانسی بررسی می‌کند. تبدیل فوریه در مواردی همچون پردازش سیگنال و نویز، پردازش تصویر، پردازش سیگنال صوتی و... کاربرد دارد. SciPy ماژول FFTPack (Fast Fourier Transform) را برای محاسبه‌ی تبدیل فوریه به کار می‌گیرد و به کاربر امکان تبدیل فوریه از طریق الگوریتم تبدیل سریع فوریه را می‌دهد.

در ادامه مثالی از یک تابع سینوسی را که تبدیل فوریه را با استفاده از ماژول FFTPack انجام می‌دهد، با هم بررسی می‌کنیم.

تبدیل سریع فوریه

تبدیل سریع فوریه را با جزییات بیشتری شرحی می‌دهیم. تبدیل فوریه گسسته یکی از تکنیک‌های ریاضی و محاسباتی است که می‌تواند داده‌ها را به داده‌هایی در محدوده‌ی فرکانسی تبدیل کند. تبدیل فوریه سریع یا همان FFT یکی از روش‌های محاسبه برای تبدیل فوریه‌ی گسسته است. FFT می‌تواند روی آرایه‌های چند بعدی اعمال شود. این نکته را یادآور می‌شویم که منظور از فرکانس، تعداد سیگنال یا طول موج در یک بازه‌ی زمانی مشخص می‌باشد.

تبدیل فوریه‌ی گسسته‌ی یک بعدی

تابع خروجی y نتیجه‌ی اعمال تبدیل فوریه‌ی سریع،یا همان تابع fft بر روی ورودی x است و طول دامنه در هر دو تابع x و y یکسان است.

#Importing the fft and inverse fft functions from fftpackage
from scipy.fftpack import fft
#create an array with random n numbers
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
#Applying the fft function
y = fft(x)
print (y)

خروجی کد بالا به شکل زیر است:

[ 4.50000000+0.j           2.08155948-1.65109876j   -1.83155948+1.60822041j -1.83155948-1.60822041j   2.08155948+1.65109876j ]

برای محاسبه‌ی معکوس تبدیل فوریه از ifft() استفاده می‌کنیم:

#FFT is already in the workspace, using the same workspace to for inverse transform
yinv = ifft(y)
print (yinv)

خروجی این کد به شکل زیر است:

[ 1.0+0.j   2.0+0.j   1.0+0.j   -1.0+0.j   1.5+0.j ]

حال مثال کاربردی‌تری را باهم بررسی می‌کنیم. به تابع زیر که به کمک کتابخانه‌ی matplotlib آن را ترسیم کرده‌ایم، توجه کنید. شکل حاصل نشانگر تابع متناوب سینوسی sin(20 × 2πt) است.

%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np 
#Frequency in terms of Hertz
fre  = 5 
#Sample rate
fre_samp = 50
t = np.linspace(0, 2, 2 * fre_samp, endpoint = False )
a = np.sin(fre  * 2 * np.pi * t)
figure, axis = plt.subplots()
axis.plot(t, a)
axis.set_xlabel ('Time (s)')
axis.set_ylabel ('Signal amplitude')
plt.show()

خروجی تابع به شکل زیر است:

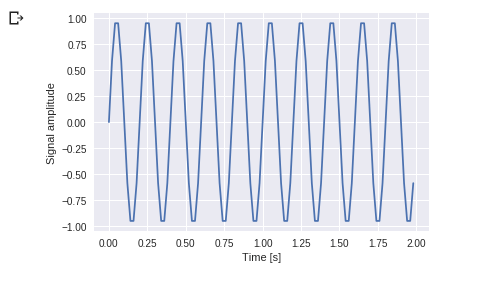
همان طور که می‌بینید فرکانس 5 هرتز است و سیگنال در 1/5 ثانیه تکرار می‌شود که دوره‌ی زمانی تناوب این سیگنال است.

حال به کمک ابزار ارئه شده در scipy از این موج سینوسی برای تبدیل فوریه استفاده می‌کنیم:

from scipy import fftpack
A = fftpack.fft(a)
frequency = fftpack.fftfreq(len(a)) * fre_samp
figure, axis = plt.subplots()
axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-fre_samp / 2, fre_samp/ 2)
axis.set_ylim(-5, 110)
plt.show()

خروجی کد بالا به شکل زیر است:

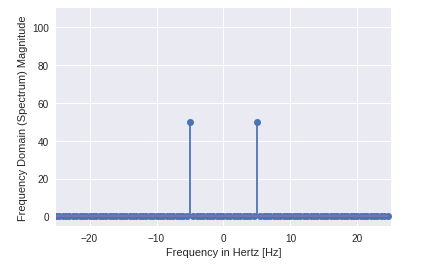
نحوه‌ی کار با ورودی و خروجی در SciPy چیست

پکیج scipy.io توابع بسیار گسترده‌ای را برای کار با انواع مختلفی از فرمت‌های داده در اختیار می‌گذارد. داده‌ها می‌توانند فرمت‌هایی مانند Matlab، IDL، MatrixMarket، Wave، Arff، Netcdf و غیره داشته باشند. در ادامه در خصوص داده‌ی Matlab جزییات بیشتری را شرح می‌دهیم.

در جدول زیر توابع به کار رفته برای بارگذاری و ذخیره‌ی یک فایل متلب (.mat) را می‌بینید:

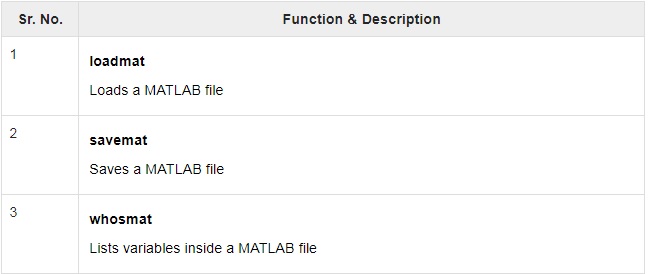
مثال زیر را در نظر بگیرید:

import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print (mat_file_content)

خروجی دستورات بالا به شکل زیر است که آرایه‌ی ورودی را به همراه متادیتا، نمایش می‌دهد.

{   'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',   '__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30   09:49:32 2017', '__globals__': [] }

اگر بخواهیم محتویات فایل متلب را بدون خواندن داده‌ها در حافظه بررسی کنیم از دستور whosmat به شکل زیر استفاده می‌کنیم:

import scipy.io as sio
mat_file_content = sio.whosmat(‘array.mat’)
print (mat_file_content)

کد بالا خروجی زیر را تولید می‌کند:

[('vect', (1, 10), 'int64')]

جبرخطی در SciPy

SciPy با استفاده از کتابخانه‌های ATLASLAPACK و BLAS ساخته شده ‌است و قابلیت‌های بسیار خوبی در زمینه‌ی جبر خطی دارد. در تمامی این روال‌های جبر خطی، انتظار می‌رود که هر شی‌ای قابل تبدیل به یک آرایه‌ی دو بعدی باشد و خروجی تمامی این روال‌ها نیز آرایه‌ای دو بعدی است.

تفاوت جبر خطی در NumPy و SciPy چیست

کتابخانه‌ی SciPy شامل تمامی موارد و توابع جبر خطی تعریف شده در NumPy است. علاوه بر آن جبر خطی در SciPy که آن را با scipy.linalg فراخوانی می‌کنیم، توابع پیشرفته‌ای دارد که در NumPy موجود نیست. کتابخانه‌ی SciPy همواره با پشتیبانی BLAS/LAPACK، کامپایل می‌شود در حالی که این گزینه در NumPy اختیاری است. در نتیجه بسته به نحوه‌ی نصب NumPy، ممکن است نسخه‌ی SciPy سریع‌تر باشد.

معادلات خطی

برای حل معادله‌ی a*x+b*y=z به ازای مقادیر مجهول x و y از ویژگی scipy.linalg.solve استفاده می‌کنیم. برای مثال فرض کنید باید معادله‌ی زیر را حل کنید:

x + 3y + 5z=10

2x + 5y + z=8

2x + 3y + 8z= 3

برای حل معادله‌ی بالا برای مقادیر مجهول x، y و z ماتریس ضرایب را در متغیر a و ماتریس سمت راست معادلات را در متغیر b قرار می‌دهیم. متغیرهای a و b را به عنوان پارامتر به تابع linalg.solve ارسال می‌کنیم و از پاسخ معادله‌ی حل شده به کمک دستور print خروجی می‌گیریم.

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy arrays
a = np.array([[1, 3, 5], [2, 5, 1], [2, 3, 8]])
b = np.array([10, 8, 3])
#Passing the values to the solve function
x = linalg.solve(a, b)
#printing the result array
print (x)

برنامه‌ی بالا خروجی زیر را برای متغیرهای x و y وz تولید می‌کند.

array([ 2., -2., 9.])

محاسبه‌ی دترمینان:

دترمینان ماتریس مربعی A به شکل |A| نمایش داده می‌شود و مقداری است که در بسیاری از محاسبات جبری به کار گرفته می‌شود. در پکیج SciPy با دستور det() این مقدار را محاسبه می‌کنیم. این تابع ماتریسی را به عنوان ورودی گرفته، و مقداری عددی را به عنوان خروجی محاسبه و برمی‌گرداند. به مثال زیر توجه کنید.

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the det function
x = linalg.det(A)
#printing the result
print (x)

خروجی برنامه به شکل زیر است.

-2.0

مقادیر ویژه و بردار ویژه:

مسأله‌ی مقدار ویژه – بردار ویژه از مسائل پرکاربرد و رایج‌ به کار گرفته شده در عملیات جبر خطی است. می‌توان مقادیر ویژه (لاندا در معادله‌ی زیر) و بردار ویژه‌ی متناظر آن (V) برای یک ماتریس مربعی را به شکل معادله‌ی زیر در نظر گرفت

تابع scipy.linalg.eig مقدار ویژه را با توجه به مسأله‌ی بردار ویژه‌ی عام محاسبه می‌کند. این تابع مقادیر ویژه و بردار ویژه را محاسبه می‌کند.به مثال زیر توجه کنید.

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the eig function
l, v = linalg.eig(A)
#printing the result for eigen values
print l
#printing the result for eigen vectors
print (v)

خروجی کد بالا به شکل زیر است:

array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values array([[-0.82456484, -0.41597356], #--Eigen Vectors       [ 0.56576746, -0.90937671]])

تجزیه‌ی مقدار منفرد یا SVD

مساله‌ی تجزیه‌ی مقدار منفرد یا SVD (Singular Value Decomposition)  می‌تواند به عنوان تعمیم مساله‌ی مقدار ویژه در ماتریس‌هایی که مربعی نیستند، در نظر گرفته شود.

تابع Scipy.linalg.svd ماتریس ورودی 'a' را به دو ماتریس واحد 'U' و 'Vh' و آرایه‌ی یک بعدی 's' تجزیه می‌کند که 's' شامل مقادیر منفرد (حقیقی و نامنفی)  است. در نتیجه، a=U*S*Vh که در آن 'S' ماتریسی است که قطر اصلی آن با مقادیر آرایه‌ی 's' و سایر عناصر با عناصر صفر پر شده است. به مثال زیر توجه کنید:

#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)
#Passing the values to the eig function
U, s, Vh = linalg.svd(a)
# printing the result
print (U, Vh, s)

کد بالا، خروجی به شکل زیر تولید می‌کند:

(   array([      [ 0.54828424-0.23329795j, -0.38465728+0.01566714j,      -0.18764355+0.67936712j],      [-0.27123194-0.5327436j , -0.57080163-0.00266155j,      -0.39868941-0.39729416j],      [ 0.34443818+0.4110186j , -0.47972716+0.54390586j,      0.25028608-0.35186815j]   ]),   array([ 3.25745379, 1.16150607]),   array([      [-0.35312444+0.j , 0.32400401+0.87768134j],      [-0.93557636+0.j , -0.12229224-0.33127251j]   ]) )

پردازش تصویر با Scipy

زیرمجموعه‌ی scipy_ndimage به پردازش تصویر اختصاص داده شده است و منظور از عبارت ndimage، تصویر n بعدی است. برخی از کارهای معمول که در پردازش تصویر انجام می‌گیرد، شامل موارد زیر است:

• ورودی/خروجی و نمایش تصویر

• دست‌کاری‌های اولیه در عکس مثل برش تصویر، چرخش، تقسیم و ...

• اعمال فیلترهای روی عکس مانند حذف نویز و sharp کردن و ...

• قطعه‌بندی تصاویر یا سگمنت کردن: برچسب‌گذاری پیکسل‌ها متناسب با آبجکت‌های مختلف در عکس

• طبقه‌بندی یا کلاس‌بندی

• استخراج ویژگی

• رجیستر کردن تصاویر

حال ببینیم برخی از این مراحل با Scipy چگونه انجام می‌شوند.

باز کردن و نوشتن در فایل‌های تصویری

پکیج misc در Scipy مجموعه‌ای از عکس‌ها را با خود به همراه دارد. می‌توان از آن عکس‌ها برای آموزش کار با تصاویر و دست‌کاری و تغییر آن‌ها استفاده کرد.

from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()

برنامه‌ی بالا خروجی زیر را تولید می‌کند.

هر تصویری در فرمت خام خود ترکیبی از رنگ‌هاست که توسط اعداد در قالب ماتریس نمایش داده می‌شوند. کامپیوتر تنها بر اساس آن اعداد تصاویر را درک و دست‌کاری می‌کند. روش RGB جزو روش‌های بسیار پرکاربرد و مرسوم در نمایش داده‌هاست.

اطلاعات آماری در خصوص تصویر بالا با کد زیر قابل استخراج است:

from scipy import misc
face = misc.face(gray = False)
print (face.mean(), face.max(), face.min())

برنامه‌ی بالا خروجی زیر را تولید می‌کند که میانگین و ماکزیمم و مینیمم مقادیر از بردار RGB را استخراج می‌کند.

110.16274388631184, 255, 0

حال می‌دانیم که هر عکس از اعدادی ساخته شده است، پس هر تغییری در مقدار این اعداد، منجر به تغییر تصویر می‌شود. بیایید چند تغییر هندسی روی تصویر اعمال کنیم. از پایه‌ای‌ترین تغییرات هندسی روی تصاویر، برش یا crop کردن تصویر است. در کد زیر تصویر را از هر طرف به اندازه‌ی 1/4 برش می‌زنیم.

from scipy import misc
face = misc.face(gray = True)
lx, ly = face.shape
# Cropping
crop_face = face[lx / 4: - lx / 4, ly / 4: - ly / 4]
import matplotlib.pyplot as plt
plt.imshow(crop_face)
plt.show()

برنامه‌ی بالا، تصویر زیر را به عنوان خروجی تولید می‌کند.

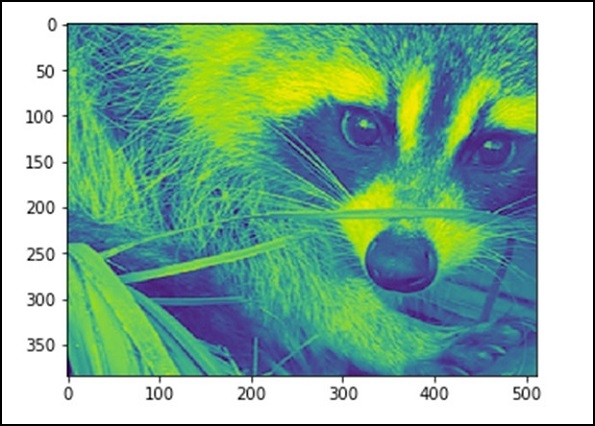
می‌توانیم تصویر خود را در جهت بالا به پایین بچرخانیم. به کد زیر توجه کنید:

# up <-> down flip
from scipy import misc
face = misc.face()
flip_ud_face = np.flipud(face)
import matplotlib.pyplot as plt
plt.imshow(flip_ud_face)
plt.show()

کد بالا تصویر را مانند شکل زیر می‌چرخاند:

همچنین از تابع rotate() می‌توان برای چرخاندن عکس با مقدار زاویه‌ی دلخواه استفاده کرد:

# rotation
from scipy import misc,ndimage
face = misc.face()
rotate_face = ndimage.rotate(face, 45)
import matplotlib.pyplot as plt
plt.imshow(rotate_face)
plt.show()

خروجی به شکل زیر است:

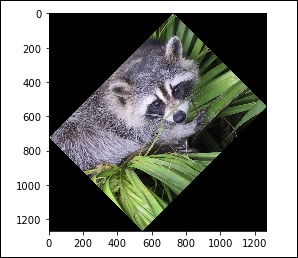
فیلترگذاری در تصاویر

بیایید در مورد اینکه فیلترها چگونه در پردازش تصویر به ما کمک می‌کنند، بحث کنیم. فیلترگذاری تکنیکی برای اصلاح یا تقویت یک تصویر است. برای مثال، می‌توانید تصویری را به منظور تاکید روی ویژگی‌های خاص یا حذف برخی ویژگی‌های دیگر، فیلتر کنید. عملیات پردازش تصویر که با فیلتر انجام می‌شود شامل صاف کردن (smoothing)، تیز کردن (sharpening) و تقویت لبه‌های تصویر (Edge Enhancement) است.

فیلترینگ تصاویر یک عملیات همسایگی (neighborhood operation) محسوب می‌شود، به این معنی که مقدار هر پیکسل در تصویر خروجی از طریق اعمال الگوریتم‌هایی روی پیکسل ورودی و پیکسل‌های موجود در همسایگی آن ورودی تعیین می‌شود. بگذارید اکنون عملیات جدیدی به کمک Scipy.ndimage انجام دهیم.

Bluring : محو و تارشدن تصویر

Blur کردن تصاویر به منظور کاهش داده‌ی نویز است. می‌توان فیلتر را اعمال و تغییرات را مشاهده کنید. مثال زیر را در نظر بگیرید:

from scipy import misc
face = misc.face()
blurred_face = ndimage.gaussian_filter(face, sigma=3)
import matplotlib.pyplot as plt
plt.imshow(blurred_face)
plt.show()

خروجی کد بالا به شکل تصویر زیر است:

مقدار پارامتر sigma بیانگر سطح محوشدگی یا Blur تصویر روی مقیاس پنج است. می‌توان با تنظیمات مختلف مقدار sigma، تغییرات حاصل را روی وضوح تصویر دید.

تشخیص لبه‌های تصویر: Edge Detection

تشخیص لبه‌ی تصاویر تکنیکی در پردازش تصویر است که برای یافتن مرز و محدوده‌ی اشیا (Object) موجود در تصویر به کار می‌آید. این کار از طریق شناسایی ناپیوستگی‌ها در مقدار روشنایی پیکسل صورت می‌گیرد. تشخیص لبه برای قطعه‌بندی تصاویر و استخراج داده در مباحثی همچون پردازش تصویر، بینایی کامپیوتر و بینایی ماشین مورد استفاده قرار می‌گیرد.

بیشترین الگوریتم‌های مورد استفاده در تشخیص لبه‌ی تصاویر عبارتند از:

• Sobel

• Canny

• Prewitt

• Roberts

• Fuzzy Logic Methods

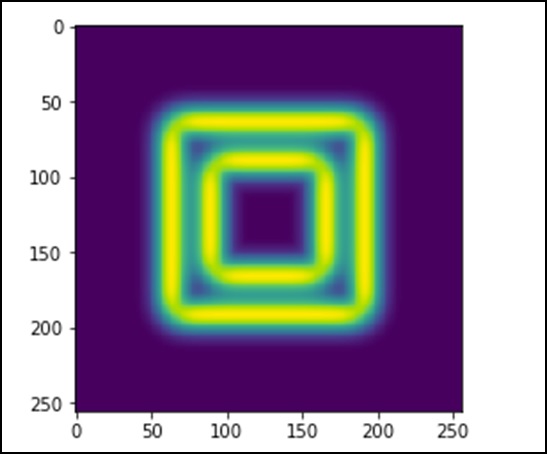
به مثال زیر توجه کنید:

import scipy.ndimage as nd
import numpy as np
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
import matplotlib.pyplot as plt
plt.imshow(im)
plt.show()

کد بالا تصویری به شکل زیر برای ما تولید می‌کند:

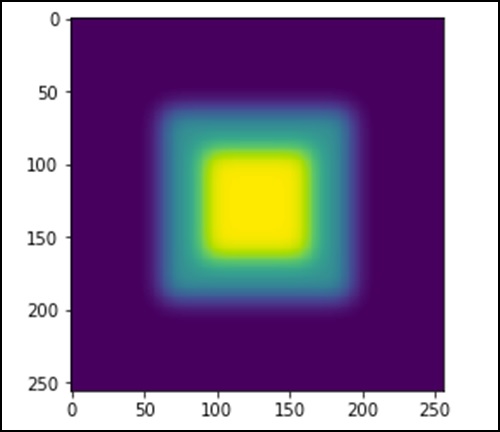
تصویر شبیه بلوک‌های مربعی با رنگ‌های مختلف است. حال ما لبه‌های هر مربع رنگی را شناسایی خواهیم کرد. در اینجا ndimage تابعی تحت عنوان Sobel را فراخوانی می‌کند تا لبه‌ها را به کمک این الگوریتم تشخیص دهد. از تابع Hypot برای ترکیب دو ماتریس حاصل با یکدیگر استفاده می‌کنیم.

import scipy.ndimage as nd
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()

نتیجه‌ی حاصل به شکل زیر است که در آن لبه‌ها و مرز آبجکت‌های موجود در تصویر که همان مربعات رنگی ما هستند، مشخص شده‌اند.

بهینه‌سازی با Scipy

پکیج scipy.optimize چندین الگوریتم بهینه‌سازی رایج و پرکاربرد را فراهم می‌کند. این ماژول ویژگی‌های زیر را دارد.

• مینیمم‌سازی نامحدود و محدود توابع چندمتغیره (تابع minimiza() ) با استفاده از الگوریتم‌های متنوع (مثل SLSQ, COBYLA, BFGS, Nelder-Mead Simplex و ...)

• روتین‌های بهینه‌سازی سراسری (مانند anneal() ، basinhopping() )

• الگوریتم‌های مینیمم‌سازی حداقل مربعات (leastsq()) و curve fitting (curve_fit())

• مینیمم‌کننده‌های توابع تک‌متغیره‌ی عددی (minimize_scalar()) و ریشه‌یاب‌ها (newton())

• حل‌کننده‌های معادلات چندمتغیره (root()) با استفاده از انواع الگوریتم‌ها (مثل هیبرید پاول، لونبرگ-مارکارت یا متدهایی در مقیاس بزرگ همچون نیوتن-کریلوف)

در ادامه برخی از توابع را برای آشنایی بیشتر شما بررسی می‌کنیم.

الگوریتم مینیمم‌سازی Nelder – Mead

تابع minimize() یک اینترفیس معمول را برای الگوریتم‌های مینیمم‌سازی توابع عددی چندمتغیره فراهم می‌کند. الگوریتم Nelder – Mead را با مقداردهی عبارت 'Nelder-Mead' به پارامتر method، می‌توان فراخوانی کرد. این الگوریتم برای مینیمم‌سازی توابع well-behaved خوب عمل می‌کند، ولی برای ارزیابی‌های گرادیان و مشتق به علت افزایش احتمالی زمان محاسبات گزینه‌ی خوبی نیست. مثال زیر را در نظر بگیرید:

import numpy as np
from scipy.optimize import minimize
#define function f(x)
def f(x):   
    return .4*(1 - x[0])**2
optimize.minimize(f, [2, -1], method="Nelder-Mead")

خروجی به شکل زیر است:

final_simplex: (array([[ 1.        , -1.27109375],       [ 1.        , -1.27118835],       [ 1.        , -1.27113762]]), array([0., 0., 0.]))           fun: 0.0       message: 'Optimization terminated successfully.'          nfev: 147           nit: 69        status: 0       success: True             x: array([ 1.        , -1.27109375])

محاسبه‌ی حداقل مربعات

Least_square برای حل مسأله‌ی غیرخطی حداقل مربعات با محدودیت‌های تعیین شده برای متغیرهاست. تابع حداقل مربعات، مینیمم اختلاف میان مقادیر دو تابع است که گاه تابع هزینه نیز نامیده می‌شود. در مثال زیر به دنبال یافتن مینیمم مقدار تابع rosenbrock بدون در نظر گرفتن محدودیت روی متغیرهای مستقل آن یعنی x0 و x1 هستیم.

#Rosenbrock Function
def fun_rosenbrock(x):
   return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)
print (res)

خروجی کد بالا به شکل زیر است:

active_mask: array([ 0., 0.])      cost: 9.8669242910846867e-30      fun: array([ 4.44089210e-15, 1.11022302e-16])      grad: array([ -8.89288649e-14, 4.44089210e-14])      jac: array([[-20.00000015,10.],[ -1.,0.]])   message: '`gtol` termination condition is satisfied.'      nfev: 3      njev: 3   optimality: 8.8928864934219529e-14      status: 1      success: True         x: array([ 1., 1.])

طبق نتیجه، در نقطه‌ی [1,1]=[x1,x0]  تابع هزینه کمترین مقدار را دارد. جمع‌بندی

در این مقاله به معرفی تابع SciPy پرداختیم. این تابع بر پایه‌ی پکیج NumPy است و ساختار داده‌ی آن مبتنی بر آرایه است. امکانات بسیار گسترده‌ای همچون معادلات جبری، پردازش تصویر، بهینه‌سازی و... در اختیار کاربران قرار می‌دهد. با مطالعه‌ی این مقاله شما متوجه شدید که SciPy چیست و با زمینه‌های کاربردی این پکیج آشنا شدید و بهتر است برای تسلط بیشتر با توجه به نیاز خود داکیومنت اصلی آن را مطالعه کنید.

اگر دوست داری به یک متخصص داده کاوی اطلاعات با زبان پایتون تبدیل شوی و با استفاده از آن در بزرگترین شرکت‌ها مشغول به کار شوی، شرکت در دوره جامع آموزش دیتا ساینس را پیشنهاد می‌کنیم.