اگر با هوش مصنوعی آشنایی داشته باشید و عنوان شبکه‌های عصبی مصنوعی (ANN: Artificial Neural Network) به گوشتان خورده باشد، احتمالاً این سؤال برای شما پیش آمده است که شبکه‌ی عصبی چیست، توانایی انجام چه کارهایی را دارد و کاربرد آن در چه زمینه‌هایی است؟ شبکه‌های عصبی، پایه و اساس یادگیری عمیق (Deep Learning) هستند. یادگیری عمیق یکی از زیرشاخه‌های یادگیری ماشین است که توانسته پیشرفت‌های زیادی به‌دست آورد. از جمله مثالهای کاربردی آن می‌توان به کنترل بازیکنان در بازی‌های Go و Poker و همچنین تسریع کشف مواد مخدر و کمک به اتومبیل‌های اتوماتیک (خودران) اشاره کرد.
اگر این نوع برنامه‌های پیشرفته شما را به هیجان بیاورند، احتمالاً به موضوع یادگیری عمیق علاقه‌مند هستید. با این حال، این امر مستلزم آن است که شما با عملکرد شبکه‌های عصبی آشنا باشید. هدف ما این است که در این مقاله‌ی آموزشی، شبکه‌های عصبی را با زبان و مفاهیم ساده، به صورت عمیق، کاربردی و سریع به شما آموزش دهیم. در این آموزش مفاهیم، کد و ریاضیاتی ارائه میشود که به شما امکان ساخت و درک یک شبکه‌ی عصبی ساده را به صورت عملی می‌دهد.
برخی از مقالات آموزشی فقط بر روی کدنویسی متمرکز هستند و از ریاضیات صرف نظر می‌کنند. اما توجه داشته باشید این موضوع مانع درک صحیح مطلب میشود. در این مقاله، آموزش‌ها را با بیان دقیق جزئیات جلو می‌بریم. با این حال برای درک مطالب لازم است که با مفاهیمی چون ماتریس‌ها و مشتق در ریاضیات آشنایی داشته باشید. کدهای مقاله با زبان پایتون نوشته شده‌اند، بنابراین اگر اطلاعات پایه‌ای از نحوه‌ی کار پایتون داشته باشید، برایتان مفید خواهد بود. به شما پیشنهاد می‌کنیم در صورت نیاز، آموزش‌های ارائه شده در سایت درخصوص توابع پایتون، حلقه‌ها و اصول کتابخانه‌ی Numpy را مطالعه کنید.
شبکه‌ی عصبی مصنوعی چیست؟
شبکه‌های عصبی مصنوعی (ANN)، یک پیاده‌سازی نرم‌افزاری از ساختار عصبی مغز ما هستند. نیازی نیست که در مورد زیست‌شناسی پیچیده‌ی ساختارهای مغزی خود صحبت کنیم، اما کافی است بدانیم که مغز حاوی سلول‌های عصبی (نورون‌هایی) است که به نوعی مانند سوئیچ‌های آلی (ارگانیک) هستند. یعنی به عنوان واسطی میان مجموعه‌ای از ورودی‌ها و خروجی قرار گرفته‌اند. این نورون‌ها بسته به قدرت ورودی الکتریکی یا شیمیایی آن‌ها می‌توانند حالت خروجی خود را تغییر دهند.
شبکه‌ی عصبی در مغز یک فرد، یک شبکه‌ی کاملاً متصل به سلول‌های عصبی (نورون‌ها) است که در آن خروجی هر نورون مشخص ممکن است که ورودی هزاران نورون دیگر باشد. یادگیری، با فعال‌سازی مکرر برخی اتصالات عصبی بر روی دیگر اتصالات رخ می‌دهد و این فعال‌سازی‌های مکرر، آن اتصال‌ها را تقویت می‌کند. این امر باعث میشود با توجه به هر ورودی مشخص، نتیجه‌ی مطلوبی ایجاد شود. این یادگیری نیازمند بازخورد (فیدبک) است. وقتی نتیجه‌ی مطلوب رخ می‌دهد، ارتباطات عصبی که آن نتیجه را ایجاد کرده‌اند، تقویت می‌شوند. شبکه‌های عصبی مصنوعی سعی در ساده‌سازی و تقلید از این رفتار مغز دارند. می‌توان آن‌ها را به دو شیوه‌ی نظارت شده (supervised) و بدون نظارت (unsupervised) آموزش داد. در یک شبکه‌ی ANN تحت نظارت، شبکه با تهیه‌ی نمونه‌های داده‌ی ورودی و خروجی تطبیق داده شده، آموزش می‌بیند. با این هدف که ANN بتواند خروجی مطلوبی را برای یک ورودی معین فراهم کند. یک مثال، فیلتر اسپم پست الکترونیکی است. داده‌ی آموزش ورودی می‌تواند تعداد کلمات مختلف در متن ایمیل باشد و داده‌های آموزش خروجی، می‌تواند این طبقه‌بندی باشد که آیا ایمیل واقعاً اسپم بوده است یا خیر.
اگر نمونه‌های زیادی از نامه‌های الکترونیکی از طریق شبکه‌ی عصبی منتقل شده باشند، این امکان را به شبکه می‌دهد تا یاد بگیرد که کدام داده‌های ورودی باعث میشود نامه‌ی الکترونیکی اسپم باشد یا نباشد. این یادگیری برای تنظیم وزن اتصالات ANN صورت می‌گیرد، اما درباره‌ی این موضوع در بخش بعدی بیشتر بحث خواهد شد. یادگیری بدون نظارت در ANN برای این است که "درک" ساختار داده‌های ورودی ارائه شده به ANN "به خودی خود" صورت گیرد. این نوع از ANN در این مقاله بررسی نخواهد شد.
ساختار شبکه‌ی عصبی مصنوعی (ANN)
در ادامه با اجزای ساختار شبکه‌ی عصبی مصنوعی آشنا می‌شویم.
نورون مصنوعی
نورون بیولوژیکی توسط یک تابع فعال‌سازی در ANN شبیه‌سازی میشود. در وظایف طبقه‌بندی (به عنوان مثال شناسایی نامه‌های الکترونیکی اسپم)، این عملکرد فعال‌سازی باید دارای ویژگی "switch on" یا "روشن شدن" یا "فعال شدن" باشد. به عبارت دیگر، هنگامی که ورودی از مقدار مشخصی بزرگتر باشد، خروجی باید تغییر کند یعنی به طور مثال از 0 به 1، از 1- به 1 یا از 0 به مقداری بزرگتر از صفر تغییر حالت دهد. این در واقع، شبیه‌سازی روشن شدن یا فعال شدن یک نورون بیولوژیکی است. یک تابع فعال‌سازی که معمولا استفاده میشود تابع سیگموئید است. در تابع سیگموئید داریم:
کد این تابع به شکل زیر است:
import matplotlib.pylab as plt
import numpy as np
x = np.arange(-8, 8, 0.1)
f = 1 / (1 + np.exp(-x))
plt.plot(x, f)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()که خروجی به این شکل است:
همانطور که در تصویر بالا مشاهده میشود، این تابع زمانی که ورودی x از یک مقدار مشخص بزرگتر باشد "فعال" میشود، یعنی از 0 به 1 حرکت می‌کند. تابع سیگموئید یک تابع پله‌ای نیست، لبه "نرم" است و خروجی به یکباره تغییر نمی‌کند. این بدان معنی است که مشتق تابع وجود دارد و این برای الگوریتم آموزش بر مبنای گرادیان مهم می‌باشد.
گره‌ها
همانطور که پیش از این ذکر شد، نورون‌های بیولوژیکی به صورت شبکه‌های سلسله مراتبی به هم متصل هستند و خروجی برخی از سلول‌های عصبی به ورودی دیگر سلول‌ها متصل است. ما می‌توانیم این شبکه‌ها را به صورت لایه‌های متصل از گره‌ها نشان دهیم. هر گره چند ورودی وزن‌دار می‌گیرد، تابع فعال‌سازی را روی حاصل جمع وزن‌دار این ورودی‌ها اعمال می‌کند و با این کار یک خروجی تولید می‌کند. این مورد را در ادامه تحلیل و بررسی می‌کنیم. نمودار زیر را در نظر بگیرید:
شکل1) گره با ورودی‌ها
در تصویر بالا، دایره نشان دهنده‌ی گره است. گره در واقع ورودی‌های وزنی را گرفته، با هم جمع می‌کند و سپس نتیجه را به تابع فعال‌سازی وارد می‌کند. خروجی تابع فعال‌سازی در نمودار فوق با h نشان داده شده است.
توجه: در برخی مقالات و نوشته‌ها به گره‌ای که در بالا نشان داده شده است، perceptron (پرسپترون) نیز گفته میشود.
"وزن" گره چیست؟ وزن‌ها اعداد حقیقی هستند (به عنوان مثال 1 یا 0 دودویی نیستند)، که در ورودی‌ها ضرب می‌شوند (هر ورودی به وزن مربوط به خودش ضرب میشود) و سپس این حاصل‌ضرب‌ها در ورودی گره، با هم جمع می‌شوند. به عبارت دیگر، ورودی وزنی به گره فوق به صورت زیر است:
در اینجا wiوزن‌ها هستند (فعلا b را نادیده بگیرید). اما این وزن‌ها به چه مربوط هستند؟ در واقع، آن‌ها متغیرهایی هستند که در طول فرآیند یادگیری تغییر می‌کنند و همراه با ورودی، خروجی گره را تعیین می‌کنند. b وزن عنصر بایاس 1+ است. گنجاندن این بایاس انعطاف‌پذیری گره را افزایش می‌دهد که بهتر است با یک مثال آن را ثابت کنیم.
بایاس
بیایید یک گره بسیار ساده را در نظر بگیریم، گره‌ای فقط با یک ورودی و یک 
شکل 2) گره ساده
ورودی به تابع فعال‌ساز گره در این حالت، مقدار x1w1 می‌باشد. تغییر w1 در این شبکه‌ی ساده چه کاری انجام می‌دهد؟ به کد زیر توجه کنید:
w1 = 0.5
w2 = 1.0
w3 = 2.0
l1 = 'w = 0.5'
l2 = 'w = 1.0'
l3 = 'w = 2.0'
for w, l in [(w1, l1), (w2, l2), (w3, l3)]:
f = 1 / (1 + np.exp(-x*w))
plt.plot(x, f, label=l)
plt.xlabel('x')
plt.ylabel('h_w(x)')
plt.legend(loc=2)
plt.show()خروجی کد به شکل زیر است:
در اینجا می‌بینیم که تغییر وزن، شیب خروجی تابع فعال‌سازی سیگموئید را تغییر می‌دهد، که بدیهی است اگر بخواهیم نقاط قوت مختلف روابط بین متغیرهای ورودی و خروجی را مدل کنیم، مفید خواهد بود. با این حال، اگر بخواهیم خروجی تنها زمانی تغییر کند که x بزرگتر از 1 باشد، چه می‌کنیم؟ این مورد، حالتی است که بایاس وارد عمل میشود. بیایید همان شبکه را با ورودی بایاس در نظر بگیریم:
شکل 3) تأثیر بایاس
کد زیر که بایاس در آن در نظر گرفته شده را ببینید:
w = 5.0
b1 = -8.0
b2 = 0.0
b3 = 8.0
l1 = 'b = -8.0'
l2 = 'b = 0.0'
l3 = 'b = 8.0'
for b, l in [(b1, l1), (b2, l2), (b3, l3)]:
f = 1 / (1 + np.exp(-(x*w+b)))
plt.plot(x, f, label=l)
plt.xlabel('x')
plt.ylabel('h_wb(x)')
plt.legend(loc=2)
plt.show()خروجی کد به شکل زیر است که تأثیر تنظیم مقادیر بایاس را نشان می‌دهد:
در این حالت، مقدار برای شبیه‌سازی عملکرد تعریف شده‌ی "روشن کردن" افزایش یافته است. همانطور که مشاهده می‌کنید با تغییر "وزن" بایاس (b) می‌توانید زمان فعال شدن گره را تغییر دهید. بنابراین با افزودن بایاس می‌توان گره را به گونه‌ای ایجاد کرد که مانند یک تابع if رفتار کند. مثلاً: if (x>z) then 1 else 0.
بدون بایاس، شما نمی‌توانید مقدار z را در جمله‌ی if تغییر دهید. در حالت بدون بایاس، مقدار z همیشه حدود صفر باقی می‌ماند. اگر سعی در شبیه‌سازی روابط شرطی دارید، این مورد بسیار مفید خواهد بود.
قراردادن تمامی ساختارهای شبکه کنار همدیگر
امیدواریم توضیحات قبلی به شما نمای خوبی از چگونگی عملکرد یک گره/ نورون/ پرسپترون داده شده در یک شبکه‌ی عصبی، ارائه داده باشد. با این حال، همانطور که احتمالا می‌دانید، تعداد زیادی از این گره‌های به هم پیوسته در یک شبکه‌ی عصبی وجود دارد. این ساختارها می‌توانند به هزاران شکل مختلف وجود داشته باشند، اما متداول‌ترین ساختار ساده‌ی شبکه‌ی عصبی شامل یک لایه‌ی ورودی، یک لایه‌ی پنهان و یک لایه‌ی خروجی است. یک نمونه از چنین ساختاری را می‌توان در شکل زیر مشاهده کرد:
شکل 4) شبکه‌ی عصبی سه لایه
سه لایه‌ی شبکه در شکل بالا قابل مشاهده است. لایه‌ی یک نشان‌دهنده‌ی لایه‌ی ورودی است، جایی که داده‌های ورودی خارجی وارد شبکه می‌شوند. به لایه‌ی 2، لایه‌ی پنهان گفته میشود زیرا این لایه بخشی از ورودی یا خروجی نیست.
توجه: شبکه‌های عصبی می‌توانند لایه‌های پنهان زیادی داشته باشند، اما در این مورد برای سادگی فقط یک لایه‌ی پنهان در نظر گرفته‌ایم. در نهایت، لایه‌ی 3 لایه‌ی خروجی است. می‌توانید ارتباطات زیادی بین لایه‌ها، به ویژه بین لایه‌ی 1 (L1) و لایه‌ی 2 (L2) مشاهده کنید. همانطور که دیده میشود، هر گره در L1 با تمام گره‌های L2 ارتباط دارد، به همین ترتیب گره‌های موجود در L2 با گره منفرد L3 ارتباط دارند. هر یک از این اتصالات دارای وزن مرتبط با خود خواهند بود.
علامت‌گذاری
ریاضیات زیر نیاز به یک علامت‌گذاری کاملاً دقیق دارد تا بدانیم درباره‌ی چه چیزی صحبت می‌کنیم. علامت‌گذاری استفاده شده در اینجا، مشابه آنچه که در مقاله‌ی آموزش یادگیری عمیق استنفورد استفاده شده، می‌باشد. در معادلات پیش رو، هر یک از این وزن‌ها با علامت‌گذاری زیر مشخص می‌شوند:
(wij(l که در آن i به شماره‌ی گره اتصال در لایه‌ی l+1 و j به شماره‌ی گره اتصال در لایه‌ی l اشاره دارد.
توجه ویژه‌ای به این مورد داشته باشید. بنابراین، برای بیان اتصال بین گره 1 در لایه 1 و گره 2 در لایه 2، علامت‌گذاری وزن به صورت W21 خواهد بود. این علامت‌گذاری شاید کمی عجیب به نظر بیاید، اما همانطور که انتظار دارید، شماره‌ها در لایه‌ی l و l+1 به ترتیب هستند (با ترتیب شماره‌ی ورودی و خروجی) و نه برعکس. با این حال، هنگامی که بایاس را اضافه می‌کنید، این علامت‌گذاری معنی بیشتری پیدا می‌کند. همانطور که در شکل بالا مشاهده می‌کنید بایاس (1+) به هر یک از گره‌های لایه‌ی بعدی متصل است. بنابراین بایاس موجود در لایه‌ی 1 به تمام گره‌های موجود در لایه‌ی 2 متصل است. از آنجا که بایاس یک گره واقعی با عملکرد فعال‌سازی نیست، ورودی ندارد (همیشه مقدار 1+ را در خروجی ایجاد می‌کند).
علامت وزن بایاس(bi(l است که در آن i نشان‌دهنده‌ی شماره‌ی گره در لایه‌ی l+1 است، همانند آنچه که برای علامت‌گذاری نرمال وزن (w21(1 استفاده شد. بنابراین، وزن مربوط به اتصال بین بایاس در لایه‌ی 1 و گره دوم در لایه‌ی 2 با (b2(1 نشان داده میشود. به یاد داشته باشید، مقادیر(wji(1 و (bi(l باید در مرحله‌ی آموزش ANN محاسبه شوند. علامت خروجی گره نیز به صورت (hj(l می‌باشد، که در آن j تعداد گره را در لایه‌ی شبکه نشان می‌دهد. همانطور که در شبکه‌ی سه لایه‌ی فوق مشاهده میشود، خروجی گره 2 در لایه‌ی 2 با علامت (h2(2 مشخص شده است. اکنون که علامت‌گذاری‌ها مرتب شده‌اند، وقت آن است که نحوه‌ی محاسبه‌ی خروجی شبکه را در زمان مشخص بودن ورودی و وزن‌ها بررسی کنیم. فرآیند محاسبه‌ی خروجی شبکه‌ی عصبی با توجه به این مقادیر، روش یا فرآیند feed-forward نامیده میشود.
روش feed-forward
برای نشان دادن نحوه‌ی محاسبه‌ی خروجی از روی ورودی در شبکه‌های عصبی، بیایید با مورد خاص شبکه‌ی عصبی سه لایه‌ای که در بالا ارائه شد، شروع کنیم. در این قسمت، همان شبکه‌ی عصبی سه لایه به صورت معادله ارائه شده است. در ادامه با یک مثال و کدهای پایتون آن را به شما نشان می‌دهیم.
در معادلات فوق، ( )f به تابع فعال‌سازی گره اشاره دارد، که در این مورد، تابع سیگموئید است. در سطر اول،(h1(2 نشان دهنده‌ی خروجی گره 1 در لایه‌ی 2 می‌باشد که ورودی‌هایش به شکل زیر هستند:
این ورودی‌ها را می‌توان در نمودار اتصال سه‌لایه‌ی فوق ردیابی کرد. آن‌ها به سادگی جمع می‌شوند و سپس برای محاسبه‌ی خروجی گره اول از تابع فعال‌سازی عبور می‌کنند. برای دو گره دیگر در لایه‌ی دوم نیز به همین ترتیب عمل می‌کنیم. خط نهایی خروجی، تنها گره موجود در لایه‌ی سوم که لایه‌ی آخر است، می‌باشد و خروجی نهایی شبکه‌ی عصبی است. همانطور که مشاهده میشود، به جای استفاده از متغیرهای ورودی وزنی (x1, x2, x3)، گره نهایی، خروجی وزنی گره‌های لایه‌ی دوم (h3(2), h2(2), h1(2)) به‌علاوه‌ی بایاس وزنی را به عنوان ورودی در نظر می‌گیرد. بنابراین، در فرم معادله می‌توانید ماهیت سلسله مراتبی شبکه‌های عصبی مصنوعی را ببینید.
مثالی برای feed-forward
حال، بیایید یک مثال ساده از خروجی این شبکه‌ی عصبی در پایتون را بررسی کنیم. قبل از هر کاری بررسی کنید که آیا وزن‌های بین لایه‌ی 1 و 2، (w11(1), w12(1),…) به طور ایده‌آل برای نمایش ماتریس مناسب هستند؟
ماتریس زیر را ملاحظه کنید:
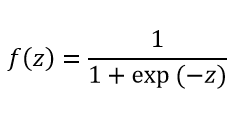
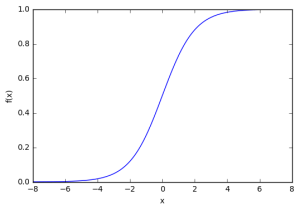
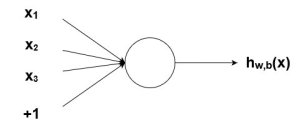
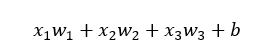
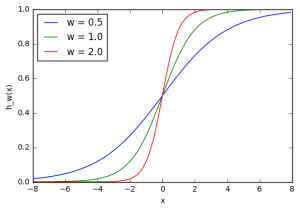
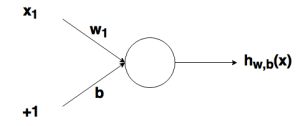
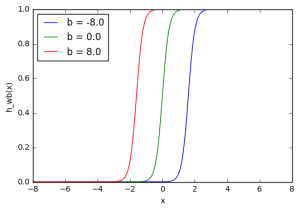
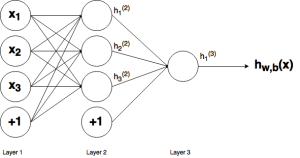
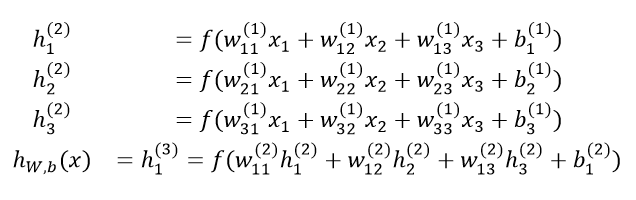
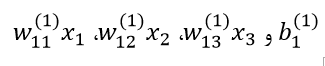
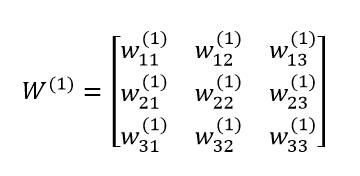این ماتریس را می‌توان با استفاده از آرایه‌های numpy به راحتی نمایش داد:
import numpy as np
w1 = np.array([[0.2, 0.2, 0.2], [0.4, 0.4, 0.4], [0.6, 0.6, 0.6]])در اینجا آرایه‌ی وزن لایه‌ی 1 را با برخی از وزن‌های نمونه پر کرده‌ایم. می‌توانیم همین کار را برای آرایه‌های وزنی لایه‌ی 2 نیز انجام دهیم:
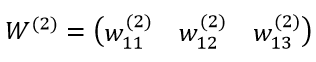کد پایتون زیر نحوه‌ی تعریف آرایه‌ی وزنی لایه‌ی 2 را نشان می‌دهد:
w2 = np.zeros((1, 3))
w2[0,:] = np.array([0.5, 0.5, 0.5])ما همچنین می‌توانیم برخی مقادیر ساختگی را در آرایه/ بردار، وزن بایاس لایه‌ی 1 و وزن بایاس لایه‌ی 2 (که فقط یک مقدار واحد در این ساختار شبکه‌ی عصبی است، یعنی یک اسکالر) تنظیم کنیم:
b1 = np.array([0.8, 0.8, 0.8])
b2 = np.array([0.2])در نهایت، قبل از نوشتن برنامه‌ی اصلی برای محاسبه‌ی خروجی از شبکه‌ی عصبی، خوب است که یک تابع پایتون جداگانه برای عملکرد فعال‌سازی تنظیم کنید:
def f(x):
return 1 / (1 + np.exp(-x))ارائه‌ی تابع feed-forward
در زیر یک روش ساده برای محاسبه‌ی خروجی شبکه‌ی عصبی، با استفاده از حلقه‌های تودرتو در پایتون آمده است. به زودی روش‌های کارآمدتر محاسبه‌ی خروجی را بررسی خواهیم کرد.
def simple_looped_nn_calc(n_layers, x, w, b):
for l in range(n_layers-1):
#Setup the input array which the weights will be multiplied by for each layer
#If it's the first layer, the input array will be the x input vector
#If it's not the first layer, the input to the next layer will be the
#output of the previous layer
if l == 0:
node_in = x
else:
node_in = h
#Setup the output array for the nodes in layer l + 1
h = np.zeros((w[l].shape[0],))
#loop through the rows of the weight array
for i in range(w[l].shape[0]):
#setup the sum inside the activation function
f_sum = 0
#loop through the columns of the weight array
for j in range(w[l].shape[1]):
f_sum += w[l][i][j] * node_in[j]
#add the bias
f_sum += b[l][i]
#finally use the activation function to calculate the
#i-th output i.e. h1, h2, h3
h[i] = f(f_sum)
return hاین تابع تعداد لایه‌های شبکه‌ی عصبی را به عنوان ورودی دریافت می‌کند که آن را به عنوان آرایه/ بردار ورودی x در نظر می‌گیریم، سپس تاپل یا لیستی از وزن‌ها و وزن‌های بایاس شبکه را دریافت می‌کند که هر عنصر در این لیست، نشان‌دهنده‌ی یک لایه‌ی l در شبکه است. به عبارت دیگر، ورودی‌ها به صورت زیر تنظیم می‌شوند:
w = [w1, w2]
b = [b1, b2]
#a dummy x input vector
x = [1.5, 2.0, 3.0]این تابع ابتدا بررسی می‌کند که ورودی به لایه‌ی گره (وزن ورودی به گره) چیست. اگر به لایه‌ی اول نگاه کنیم، ورودی گره‌های لایه‌ی دوم حاصل‌ضرب بردار ورودی x در وزن‌های مربوطه می‌باشد. بعد از لایه‌ی اول، ورودی لایه‌های بعدی، خروجی لایه‌های قبلی است. در پایان، یک حلقه‌ی تودرتو از طریق مقادیر مربوط به i و j بردارهای وزن و بایاس داریم. این تابع از ابعاد وزن‌های هر لایه برای تشخیص تعداد گره‌ها و همچنین ساختار شبکه استفاده می‌کند. فراخوانی تابع به صورت زیر است:
simple_looped_nn_calc(3, x, w, b)این تابع، خروجی 0.8354 را ایجاد خواهد کرد. ما می‌توانیم این نتایج را با انجام دستی محاسبات در معادلات اصلی تأیید کنیم:
پیاده‌سازی کارآمدتر شبکه‌ی عصبی با feed-forward
همانطور که قبلاً بیان شد استفاده از حلقه‌ها کارآمدترین روش برای محاسبه‌ی feed-forward در پایتون نیست؛ چرا که حلقه‌ها در پایتون به طرز مشهودی کند هستند. در ادامه یک مکانیزم جایگزین و کارآمدتر برای اجرای محاسبات feed-forward در پایتون و numpy مورد بحث قرار خواهد گرفت. می‌توانیم با استفاده از تابع timeit% کارایی الگوریتم ارائه شده را محاسبه کنیم. این تابع چندین بار الگوریتم را اجرا کرده و میانگین زمان‌های اجرا را، به عنوان خروجی برمی گرداند:
%timeit simple_looped_nn_calc(3, x, w, b)اجرای این کد به ما می‌گوید که اجرای محاسبات feed-forward به اندازه‌ی 40 میکروثانیه طول می‌کشد. رسیدن به نتیجه در مدت چند ده ثانیه، بسیار سریع به نظر می‌رسد، اما زمانی که این روش برای شبکه‌های عصبی بسیار بزرگ با چندصد گره در هر لایه استفاده شود، به خصوص هنگام آموزش شبکه، این سرعت قابل قبول نخواهد بود. اگر یک شبکه‌ی عصبی چهارلایه را با استفاده از همان کد امتحان کنیم، عملکرد به مراتب بدتری داریم ( 70 میکروثانیه).
بردارسازی در شبکه‌های عصبی
در روش feed forward می‌توان معادلات را به صورت فشرده‌تر نوشت و محاسبات را با کارایی بیشتری پیاده کرد. در ابتدا، یک متغیر جدید با عنوان (zi(l تعریف می‌کنیم که نشان‌دهنده‌ی مجموع ورودی‌ها به گره i در لایه‌ی l می‌باشد و شامل قسمت بایاس هم می‌باشد. بنابراین در گره اول از لایه‌ی 2 مقدار z برابر است با:
که در آن n نشان‌دهنده‌ی تعداد گره‌ها در لایه‌ی 1 می‌باشد. با استفاده از این علامت‌گذاری، مجموعه معادلات نامناسب قبلی به عنوان مثال برای شبکه‌ی سه‌لایه می‌تواند به صورت زیر کاهش یابد:
به استفاده از حرف بزرگ W برای اشاره به ماتریس وزن‌ها توجه کنید. دقت کنید تمام المان‌هایی در که معادله‌ی فوق وجود دارند، همگی ماتریس یا بردار هستند. اگر با این مفاهیم آشنایی ندارید، در بخش بعدی به طور کامل توضیح داده می‌شوند.
آیا می‌توان معادله‌ی فوق را کمی ساده‌تر کرد؟ پاسخ مثبت است. ما می‌توانیم محاسبات را از طریق هر تعداد لایه در شبکه‌ی عصبی با کلی‌سازی (generalizing) گسترش دهیم.
در اینجا می‌توانیم روند کلی feed forward را مشاهده کنیم، جایی که خروجی لایه‌ی l به ورودی لایه‌ی l + 1 تبدیل میشود. توجه کنید که (h (1 ورودی لایه‌ی x است و (h (nl ( تعداد لایه‌های شبکه nl است) خروجی لایه‌ی خروجی است.
توجه کنید که در معادلات بالا ارجاع به شماره‌ی گره i و j را حذف کرده‌ایم. اما چگونه می‌توانیم این کار را انجام دهیم؟ آیا مجبور نیستیم که در کد حلقه بزنیم و همه‌ی ورودی‌ها و خروجی‌های مختلف گره را محاسبه کنیم؟ پاسخ این است که برای انجام ساده‌تر این کار می‌توانیم از ضرب‌های ماتریسی استفاده کنیم. این فرآیند، "بردارسازی" (vectorization) نامیده میشود و دو مزیت دارد:
- اولین مزیتش این است که پیچیدگی کد را کاهش می‌دهد.
- دومین مزیت این است که ما می‌توانیم به جای استفاده از حلقه‌ها، از برنامه‌های جبر خطی سریع در پایتون (و زبان‌های دیگر) استفاده کنیم که باعث تسریع برنامه‌های ما میشود.
Numpy به راحتی می‌تواند از پس این محاسبات برآید. برای کسانی که با عملیات ماتریس آشنا نیستند، در بخش بعدی توضیح مختصری از عملیات ماتریس‌ها آمده است.
ضرب ماتریس‌ها
بیایید معادله‌ی زیر را به صورت ماتریسی / برداری برای لایه‌ی ورودی گسترش دهیم: 
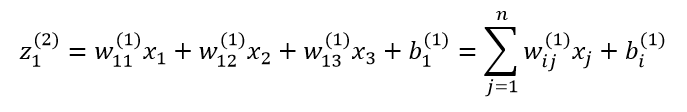
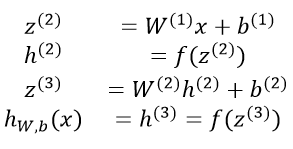
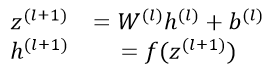
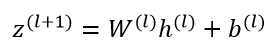توجه کنید که در این معادله h(l)=x است. گسترش معادله‌ی بالا برای لایه‌ی ورودی به شکل زیر است:
کسانی که از نحوه‌ی عملکرد ضرب ماتریس آگاهی ندارند، بهتر است که عملیات ماتریس را بررسی کنند. سایت‌های زیادی وجود دارند که این موضوع را به خوبی پوشش می‌دهند. با این حال، خیلی سریع ضرب ماتریس‌ها را بررسی می‌کنیم: وقتی ماتریس وزن در بردار لایه‌ی ورودی ضرب میشود، هر عنصر در سطر ماتریس وزن در هر عنصر در تنها ستون بردار ورودی ضرب میشود (بردارها فقط یک ستون دارند)، سپس نتیجه‌ی این ضرب‌ها با هم جمع میشود تا اینکه یک بردار 3*1 جدید ایجاد شود. سپس می‌توانید بردارهای بایاس وزن را اضافه کنید تا به نتیجه‌ی نهایی برسید. اگر دقت کنید می‌توانید مشاهده کنید که هر سطر از نتیجه‌ی نهایی بالا با تابع فعال‌سازی در مجموعه معادلات اصلی غیرماتریسی فوق مطابقت دارد. اگر تابع فعال‌سازی بتواند به عناصر اعمال شود (یعنی به هر سطر به طور جداگانه در بردار اعمال شود)، ما می‌توانیم تمام محاسبات خود را به جای حلقه‌های هسته‌ی پایتون، با استفاده از ماتریس و بردار انجام دهیم.
بیایید نگاهی به نسخه‌ی ساده‌تر (و سریع‌تر) simple_looped_nn_calc بیندازیم:
def matrix_feed_forward_calc(n_layers, x, w, b):
for l in range(n_layers-1):
if l == 0:
node_in = x
else:
node_in = h
z = w[l].dot(node_in) + b[l]
h = f(z)
return hبه سطر هفتم دقت کنید. برای ضرب وزن‌ها در بردار ورودی گره در numpy به‌جای استفاده از علامت * از علامت (a.dot(b استفاده می‌کنیم.
اگر با استفاده از این عملکرد جدید و یک شبکه‌ی ساده‌ی 4 لایه، timeit% را دوباره اجرا کنیم، فقط 24 میکروثانیه پیشرفت می‌کنیم (کاهش از 70 میکروثانیه به 46 میکروثانیه). با این حال، اگر اندازه‌ی شبکه‌ی 4 لایه را به لایه‌های 100-100-50-10-10 گره افزایش دهیم، نتایج بسیار چشم‌گیرتری به‌دست می‌آید.
روش مبتنی بر حلقه‌ی پایتون 41 میلی ثانیه طول می‌کشد. توجه داشته باشید که واحد در اینجا میلی‌ثانیه است و پیاده‌سازی برداری فقط 84 میکروثانیه طول می‌کشد تا از طریق شبکه‌ی عصبی به جلو منتقل شود. با استفاده از محاسبات برداری‌شده به جای حلقه‌های پایتون، کارایی محاسبه را 500 برابر افزایش داده‌ایم! این پیشرفت خیلی خوبی است. حتی امکان اجرای سریع‌تر عملیات ماتریس با استفاده از پکیج‌‌های یادگیری عمیق مانند TensorFlow و Theano که از GPU رایانه‌ی شما (و نه CPU) استفاده می‌کنند، وجود دارد که معماری آن برای محاسبات سریع ماتریس مناسب‌تر است.
جمع بندی:
در این مقاله به معرفی شبکه‌ی عصبی و راهکار feed-forward برای آن پرداختیم. شبکه‌های عصبی جزء الگوریتم‌های مهم در یادگیری ماشین به شمار می‌روند. علاوه بر این، برای یادگیری الگوریتم‌های جدید همچون یادگیری عمیق، آشنایی با شبکه‌های عصبی الزامی است. در این مقاله سعی شد تا علاوه بر تشریح فرمول‌های ریاضی، پیاده‌سازی کدهای مربوطه در پایتون نیز بیان شود تا درک بهتری برای خواننده فراهم شود. امیدوار هستیم که این مقاله برای شما مفید بوده باشد. خوشحال می‌شویم نظرات و تجربیات خود را با ما در میان بگذارید.
اگر به یادگیری بیشتر در زمینه‌ی برنامه نویسی پایتون علاقه داری، یادگیری زبان پایتون بسیار ساده است. و با شرکت در دوره‌ی آموزش پایتون توسعه وب در آینده می‌توانی اپلیکیشن موبایل و دسکتاپ بسازی و وارد حوزه‌ی هوش مصنوعی هم شوی.