۶ دیدگاه
کیا عابدی
۲۰ آبان ۱۴۰۲، ۱۸:۴۵
نازنین کریمی مقدم
۲۳ آبان ۱۴۰۲، ۲۰:۳۸
۲۰ آذر ۱۴۰۰، ۱۷:۲۱
نازنین کریمی مقدم
۲۱ آذر ۱۴۰۰، ۰۶:۰۶
امیر ارشیا
۱۸ اسفند ۱۳۹۹، ۱۱:۳۵
نازنین کریمی مقدم
۲۱ اسفند ۱۳۹۹، ۱۷:۰۴
دوره الفبای برنامه نویسی با هدف انتخاب زبان برنامه نویسی مناسب برای شما و پاسخگویی به سوالات متداول در شروع یادگیری موقتا رایگان شد:


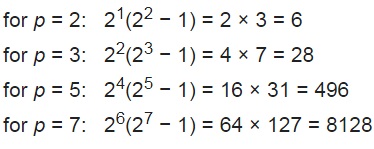 برنامه تشخیص عدد کامل در پایتون[/caption]
برنامه تشخیص عدد کامل در پایتون[/caption]


