در روز عدد پی، اِما هارکوا ایوائو عدد پی را تا 31 تریلیون رقم محاسبه کرد و رکورد قبلی که 22 رقم بود را شکست. ما عدد پی یا همان pi را تقریبا 14/3 می‌شناسیم. اما سوال اینجاست که ما این را از کجا می‌دانیم؟ چگونه عدد پی را درست می‌کنیم؟محاسبه عدد پی با پایتون چگونه است؟

روش‌های مختلفی برای محاسبه‌ی ارقام عدد پی وجود دارند. می‌توانید از نمونه‌گیری تصادفی، هندسه، حساب و روش‌های دیگر استفاده کنید. اما چرا ما به این موضوع اهمیت می‌دهیم؟

با داشتن 39 رقم اول این عدد، می‌توان عرض درون یک اتم هیدروژن را بر اساس معیار سنجش پذیرفته شده‌ی جهانی، محاسبه نمود.

آیا واقعاً به 39 تریلیون رقم احتیاج داریم؟

 احتمالا نه! اما این بدان معنا نیست که این دستاورد ارزشی ندارد. برای دستیابی به چنین تقریبی، از ابزارهای بسیار مهمی در ریاضی، علوم کامپیوتر و مهندسی کامپیوتر استفاده شده است.

ما باید به سوالاتی در مورد دقت محاسبه‌ی ارقام اعشاری، صحت تخمین و مرزهای خطا و سوالات مربوط به بهینه‌سازی بپردازیم. در این مقاله به محاسبه‌ی عدد پی در پایتون می‌پردازیم. ابتدا روش‌های ریاضی ارائه شده را بررسی کرده و کد آن‌ها به زبان پایتون را می‌نویسیم. همچنین از کتابخانه‌های محاسباتی ارائه شده در این زبان نیز برای محاسبه‌ی عدد پی می‌توان بهره برد.

روش مونت-کارلو برای محاسبه‌ی عدد پی

کار را با روش مونت-کارلو آغاز می‌کنیم. این روش‌ها، برای تولید نتایج عددی، به نمونه‌گیری تصادفی متکی هستند. برای رسیدن به هدف، ما می‌خواهیم نقاطی را در صفحه x-y نمونه‌برداری کنیم. به شکل زیر نگاه کنید. یک دایره به شعاع 1 در یک مربع احاطه شده است. طول ضلع این مربع دقیقا برابر قطر دایره است که برابر با 2 می‌باشد.

[caption id="attachment_74730" align="alignnone" width="700"]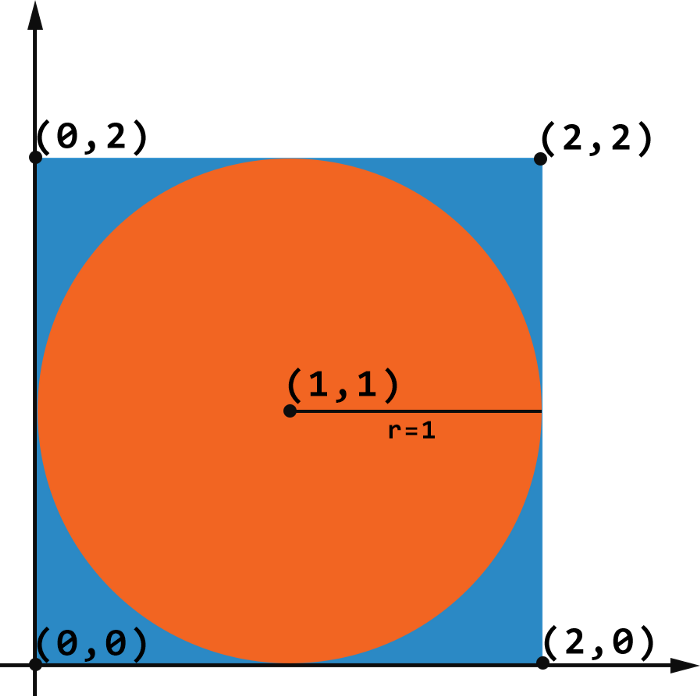 محاسبه عدد پی با پایتون[/caption]

حال بگذارید فرض کنیم که در حال بازی به شرح زیر هستیم:

یک نقطه‌ی تصادفی را در محدوده‌ی x و y انتخاب می‌کنیم. طوری که:

[caption id="attachment_74725" align="aligncenter" width="288"]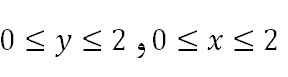 محاسبه عدد پی با پایتون[/caption]

اگر این نقطه داخل دایره باشد شما یک دلار برنده می‌شوید، در غیر این صورت من برنده می‌شوم. شانس شما برای بردن یک دلار چقدر است؟ این مقدار برابر است با نسبت ناحیه‌ی نارنجی رنگ به کل ناحیه (ناحیه نارنجی + ناحیه آبی).

[caption id="attachment_74726" align="aligncenter" width="315"]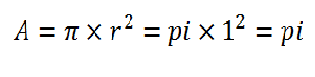 محاسبه عدد پی با پایتون[/caption] مساحت دایره برابر است با: [caption id="attachment_74727" align="aligncenter" width="218"] 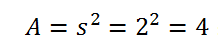محاسبه عدد پی با پایتون[/caption] مساحت کل ناحیه برابر با مساحت مربع است که برابر است با: [caption id="attachment_74728" align="aligncenter" width="132"] 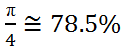محاسبه عدد پی با پایتون[/caption] بنابراین شانس شما به طور تقریبی برابر است با: که تقریب خوبی است.

بنابراین اگر یک دسته امتیاز در نظر بگیریم و درصد نقاطی که داخل دایره قرار می‌گیرند را بررسی کنیم، می‌توانیم pi را تخمین بزنیم.

این نمونه‌برداری تصادفی دقیقا همان روش مونت-کارلو است. کد زیر از ده میلیون، صد میلیون و یک میلیارد نقطه برای محاسبه‌ی pi نمونه‌برداری می‌کند.

import random
import math
def monte_carlo_estimation():
    area_circle = 1
    area_square = 1
    pi = 0
    for z in range(0, 1000000000):
        x = random.uniform(0, 2)
        y = random.uniform(0, 2)
        in_circle = math.pow((x-1), 2) + math.pow((y-1), 2) <= 1
        if in_circle:
            area_circle += 1
        area_square += 1
        pi = 4 * (area_circle / area_square)
    print("Estimate: " + str(pi))
if __name__ == '__main__':
    monte_carlo_estimation()

که خروجی کد برای نقاط نمونه‌ی انتخابی به شکل زیر است:

این نتیجه چندان هم بد نیست. یک میلیارد تکرار در کامپیوتر ما حدودا نیم ساعت طول می‌کشد و به ما تخمینی از pi می‌دهد که فقط 0.00007 خطا دارد.

اما فعلا از تولید 31 تریلیون رقم عدد pi فاصله‌ی زیادی داریم. خوشبختانه روش‌های بسیار زیادی برای تست و تلاش وجود دارد.

یک روش محاسباتی برای عدد Pi

[caption id="attachment_74732" align="aligncenter" width="199"]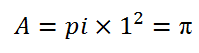 محاسبه عدد پی با پایتون[/caption] می‌دانیم که مساحت یک دایره به شعاع 1 برابر است با:

بیایید مساحت یک دایره به شعاع 1 را محاسبه کنیم.

سوال: چگونه می‌توانیم مساحت یک دایره را کاملا دقیق محاسبه کنیم؟

ما می‌توانیم این کار را به کمک انتگرال‌ها انجام دهیم. به شکل زیر نگاه کنید.

این شکل، قسمت فوقانی سمت راست از  1/4 یک دایره به شعاع 1 که به مرکز (0و0) واقع شده است را نشان می‌دهد. معادله‌ی این دایره به شکل زیر است: [caption id="attachment_74734" align="aligncenter" width="139"]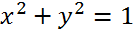 محاسبه عدد پی با پایتون[/caption] به هر حال ما فقط با قسمت بالای محور x سروکار داریم و می‌توانیم معادله را به صورت زیر بازنویسی کنیم:   [caption id="attachment_74733" align="aligncenter" width="520"]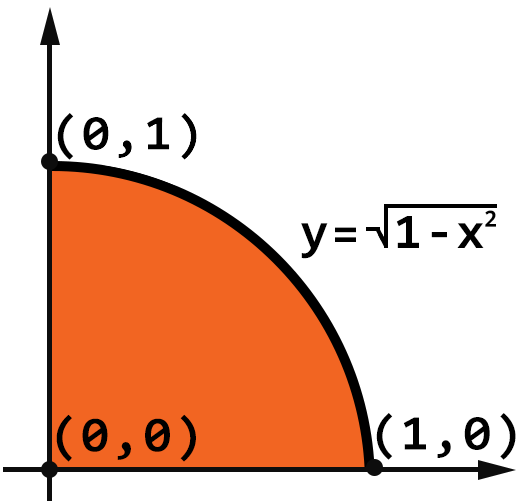 محاسبه عدد پی با پایتون[/caption]

از آنجا که مساحت کل دایره، Pi است مساحت قسمت نشان داده شده Pi/4 می‌باشد. می‌توانیم انتگرال از 0 تا 1 را برای معادله‌ی فوق محاسبه کنیم و این انتگرال برابر Pi/4 می‌باشد.

و اما باز هم یک سوال؟

انتگرال‌گیری از یک تابع، حقیقتا چه مفهومی دارد؟

ساقه‌های انتگرال مجموع ریمان، توسط برنهارد ریمان ساخته شده است. (1826)

مجموع ریمان به ما این اجازه را می‌دهد تا انتگرال‌ها را با جمع کردن مثلث‌های پایین منحنی، به صورتی که در شکل زیر نشان داده شده است، تقریب بزنیم:

هر چه تعداد مثلث‌هایی که استفاده می‌کنیم بیش‌تر باشد، تخمین بهتری خواهیم داشت:

[caption id="attachment_74735" align="aligncenter" width="700"]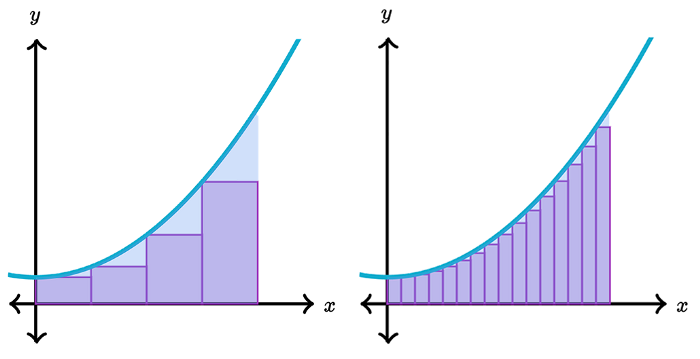 محاسبه عدد پی با پایتون[/caption] کد زیر از روش مجموع ریمان، برای تخمین مساحت زیر دایره استفاده می‌کند. این تقریب برابر Pi/4 می‌باشد.

import math
import time
def left_endpoint_riemann_sum():
    N = 10000000
    delta_x = (1 - 0) / N
    x = 0
    pi = 0
    while x < 1:
        f_x = math.sqrt(1 - math.pow(x, 2))
        pi += f_x * delta_x
        x += delta_x
    pi = 4 * pi
    print("Estimate: " + str(pi))
    print("Actual:   " + str(math.pi))
def midpoint_riemann_sum():
    N = 1000000000
    delta_x = (1 - 0) / N
    x = 0
    pi = 0
    start = time.time()
    while x < (1-delta_x):
        x_next = x + delta_x
        x_mid = (x_next + x) / 2
        f_x = math.sqrt(1 - math.pow(x_mid, 2))
        pi += f_x * delta_x
        x += delta_x
    pi = 4 * pi
    end = time.time()
    print(end - start)
    print("Estimate: " + str(pi))
    print("Actual:   " + str(math.pi))
if __name__ == '__main__':
    left_endpoint_riemann_sum()

و نتایج به صورت زیر است:

این نتیجه مطمئنا پیشرفتی در روش‌های قبلی ما است.

با همان تعداد تکرار، تعداد رقم‌های اعشار درست بیش‌‌تری را کسب کرده‌ایم.

ولی باز هم می‌توانیم عملکرد بهتری داشته باشیم!

روش مجموع بی‌نهایت در محاسبه‌ی عدد Pi

ایده‌ی مجموع بی‌نهایت، به نظر کاربردی‌تر می‌آید. بنابراین ما این مسیر را ادامه می‌دهیم. از مثلثات می‌دانیم که tan(pi/4)=1 است. اکنون می‌توانیم تابع معکوس تانژانت را برای محاسبه‌ی (arctan(1 استفاده کنیم و داریم arctan(1)=pi/4. خوشبختانه یک فرمول ساده و آسان برای محاسبه‌ی (arctan(x داریم.

[caption id="attachment_74737" align="aligncenter" width="662"]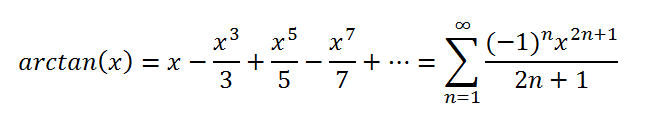 محاسبه عدد پی با پایتون[/caption]

این روش به نام گرگوری - لبینز یا مجموع ماهاوا - گرگوری شناخته شده است که به نام‌های جیمز گرگوری (1646)، گاتفرد لبینز (1638) و ماهاوا سانگراما (1340) نام‌گذاری شده است.

می‌توانیم x=1 قرار دهیم و کد زیر را اجرا کنیم:

import math
import time
def gregory_leibinz():
    pi = 0
    start = time.time()
    for x in range(0, 1000000000):
        numerator = math.pow(-1, x) * math.pow(1, 2*x+1)
        denominator = 2*x + 1
        pi += numerator/denominator
    end = time.time()
    pi = pi * 4
    print(end - start)
    print("Estimate: " + str(pi))
    print("Actual:   " + str(math.pi))
def machin():
    num_iterations = 6
    arc_tan_1_239 = arc_tan(1/239, num_iterations)
    arc_tan_1_5 = arc_tan(1/5, num_iterations)
    pi = 4 * (4*arc_tan_1_5 - arc_tan_1_239)
    print("Estimate: " + str(pi))
    print("Actual:   " + str(math.pi))
def arc_tan(x, iterations):
    arc_tan_of_x = 0
    for z in range(0, iterations):
        numerator = math.pow(-1, z) * math.pow(x, 2 * z + 1)
        denominator = 2 * z + 1
        arc_tan_of_x += numerator / denominator
    return arc_tan_of_x
if __name__ == "__main__":
    machin()

نتایج در یک گام و در یک مسیر درست می‌باشد: برای یک میلیارد تکرار، یک رقم بیشتر نسبت به روش انتگرال به دست می‌آوریم:

می‌توانیم این روش را با کمی بهبود ادامه دهیم و نتایج بسیار بهتری بگیریم: [caption id="attachment_74739" align="aligncenter" width="400"]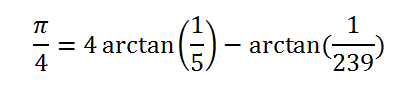 محاسبه عدد پی با پایتون[/caption] یک پیشرفت توسط جان ماشین (1706) ایجاد شده است که فرمول زیر را توسعه داده است: (استخراج و اثبات این فرمول از حوصله‌ی این مقاله خارج است. شما می‌توانید در صورت لزوم به این مقاله مراجعه کنید.)

import math
import time
def gregory_leibinz():
    pi = 0
    start = time.time()
    for x in range(0, 1000000000):
        numerator = math.pow(-1, x) * math.pow(1, 2*x+1)
        denominator = 2*x + 1
        pi += numerator/denominator
    end = time.time()
    pi = pi * 4
    print(end - start)
    print("Estimate: " + str(pi))
    print("Actual:   " + str(math.pi))
def machin():
    num_iterations = 6
    arc_tan_1_239 = arc_tan(1/239, num_iterations)
    arc_tan_1_5 = arc_tan(1/5, num_iterations)
    pi = 4 * (4*arc_tan_1_5 - arc_tan_1_239)
    print("Estimate: " + str(pi))
    print("Actual:   " + str(math.pi))
def arc_tan(x, iterations):
    arc_tan_of_x = 0
    for z in range(0, iterations):
        numerator = math.pow(-1, z) * math.pow(x, 2 * z + 1)
        denominator = 2 * z + 1
        arc_tan_of_x += numerator / denominator
    return arc_tan_of_x
if __name__ == "__main__":
    machin()

نتایج به صورت زیر می‌باشد. به تعداد تکرارها دقت کنید. با 10 تکرار، به خوبی روش قبلی تخمین زده‌ایم. روش مونت-کارلو که در قسمت اول بررسی کردیم، یک میلیارد تکرار نیاز دارد تا همان نتیجه‌ای را بگیرد که فرمول Machin در 3 مرحله به آن رسیده است.

اما همان طور که حدس می‌زنید می‌توانیم هنوز هم این نتیجه را بهبود ببخشیم و بهتر از این هم عمل کنیم.

روش مجموع بی‌نهایت بهبود یافته برای محاسبه‌ی عدد Pi

آخرین سری بی‌نهایتی که بررسی می‌کنیم، روش ریاضی‌دان سرشناس سرینواسا رامانوجان است (1887).

وی علی‌رغم این که در ابتدا تحصیلات رسمی کمی داشت، بسیاری از نظریه‌های برجسته در ریاضیات را ارائه کرد.

[caption id="attachment_74741" align="aligncenter" width="700"]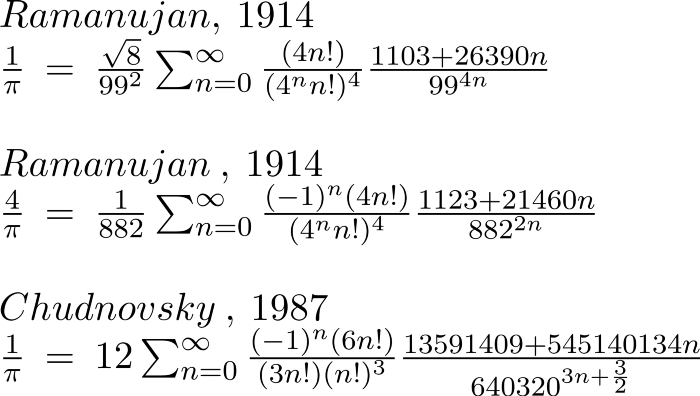 محاسبه عدد پی با پایتون[/caption]

رامانوجان دو فرمول برای محاسبه‌ی عدد pi نوشت. برادران چانوسکی، گرگوری (1952) و دیود (1947) فرمول‌های اولیه‌ی رامانوجان را بهبود بخشیدند.

کد زیر یک پیاده‌سازی از فرمول چادونوسکی است:

import math
import decimal
def madhava_leibniz():
    decimal.getcontext().prec = 50
    sqrt_12 = math.sqrt(12)
    pi = 0
    for k in range(0, 32):
        numerator = math.pow(-3, -k)
        denominator = (2*k + 1)
        pi += numerator / denominator
    pi = sqrt_12 * pi
    print("Estimate: " + str(decimal.Decimal(pi)))
    print("Actual:   " + str(math.pi))
def chudnovsky():
    pi = 0
    for k in range(0, 15):
        numerator = math.pow(-1, k % 2) * math.factorial(6*k) * (13591409 + 545140134*k)
        denominator = math.factorial(3*k) * math.pow(math.factorial(k), 3) * math.pow(640320, 3*k+3/2)
        pi += numerator / denominator
    pi = 12 * pi
    pi = 1/pi
    print("Estimate: " + str(pi))
    print("Actual:   " + str(math.pi))
if __name__ == '__main__':
    chudnovsky()

پس از یک تکرار، این فرمول، عدد را تا 14 رقم به درستی تخمین می‌زند. با هر تکرار موفق، این فرمول 14 رقم درست دیگر از Pi را تولید می‌کند.

پس از سه بار تکرار، ما در حال محاسبه‌ی عرض جهان در یک اتم هیدروژن هستیم. این فرمول، اساس هر نوع محاسبه‌ی مدرن عدد است.

معمولا برای پیاده‌سازی از y-cruncher استفاده می‌کنند. Y-cruncher نرم‌افزاری است که برای محاسبه‌ی کارآمد عدد پی طراحی شده است.

محاسبه‌ی عدد Pi با کتابخانه‌ی math در پایتون

یک روش ساده‌ی محاسبه‌ی عدد پی فراخوانی این مقدار ثابت توسط کتابخانه‌ی math است. به کد زیر توجه کنید:

# Import math Library
import math
# Print the value of pi
print (math.pi)

با این روش می‌توان عدد پی را تا دوازده رقم اعشار تولید کرد. به خروجی زیر توجه کنید:

3.141592653589793

جمع‌بندی

در این مقاله مطمئنا موارد بسیار زیادی وجود دارد که بایستی بهبود یابد. روش مونت-کارلو معرفی شده تا حد زیادی به یک انتخاب تصادفی متکی است که این فقط یک انتخاب شبه تصادفی می‌باشد. همچنین به دلیل وجود خطا در عملیات نقطه‌ی شناور، عدم دقت وجود دارد. برای افرادی که به دنبال محاسبه‌ی رقم‌های اعشاری بیش‌تری هستند کلاس Big Decimal جاوا، نقطه شروع مناسبی است.

ما 4 روش مختلف برای محاسبه‌ی عدد پی بررسی کردیم: شبیه‌سازی تصادفی، انتگرال‌گیری، توابع مثلثاتی و سری‌های بی‌نهایت.

مشکلات مربوط به تخمین زدن، ممکن است اکنون پیش پا افتاده به نظر برسند اما این مشکل به این دلیل به وجود می‌آید که ما فقط می‌توانیم یک میلیارد تکرار را در لپتاپ‌های امروزی اجرا کنیم.

در بیش‌تر زمان‌ها، یافتن برآوردهای (تخمین‌های) دقیق نیاز به فرمول‌های هوشمندانه‌ای داشت که از لحاظ محاسباتی پرهزینه نبودند.

اگر به یادگیری بیشتر در زمینه‌ی برنامه نویسی پایتون علاقه داری، یادگیری زبان پایتون بسیار ساده است. و با شرکت در دوره‌ی آموزش پایتون توسعه وب در آینده می‌تونی اپلیکیشن موبایل و دسکتاپ بسازی و وارد حوزه‌ی هوش مصنوعی هم شوی.