یه روز بارونی توی دهه ۱۹۰۰ یه دانشمند به اسم فرانسیس گالتون، دنبال راهی بود که قد بچه‌ها رو بر اساس قد والدینشون پیش بینی کنه. اون با یه عالمه داده سر و کار داشت و نمی‌دونست چطور می‌تونه از این اطلاعات استفاده مفیدی بکنه. اینجا بود که یه فکر بکر به ذهنش رسید: آیا می‌شه یه رابطه ریاضی بین این داده‌ها پیدا کرد؟

گالتون فهمید که با یه خط ساده که از بین نقاط داده‌ها می‌گذره، می‌تونه یه الگوی تقریبی برای پیش بینی قد بچه‌ها پیدا کنه. این ایده که بعدها به "رگرسیون خطی" معروف شد، یکی از اصول اساسی آمار و یادگیری ماشین شد.

رگرسیون خطی چیه؟

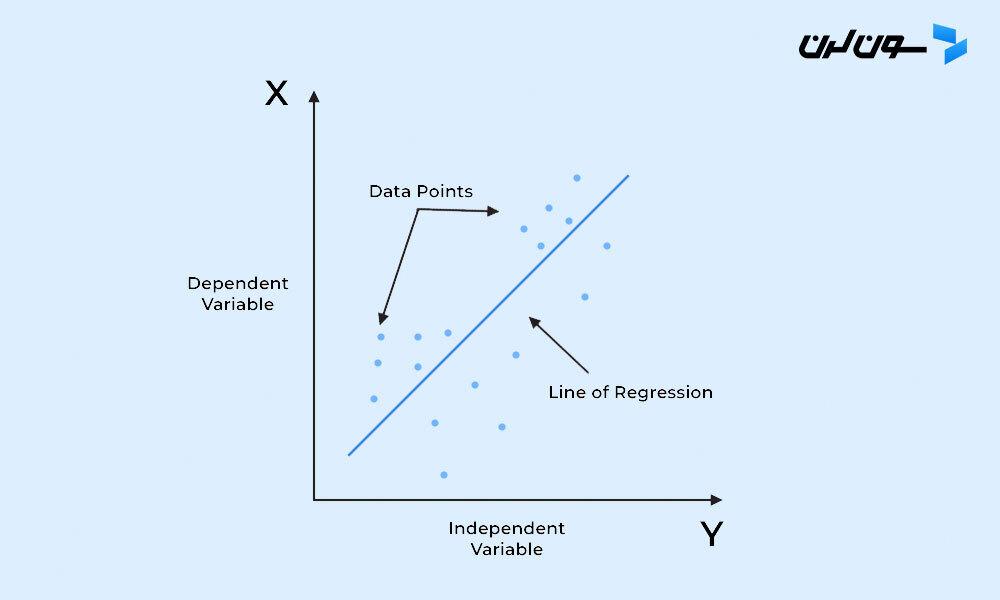
رگرسیون خطی یه روش تحلیل آماریه که برای پیش بینی مقدار یه متغیر بر اساس مقدار یه متغیر دیگه استفاده می‌شه. متغیری که می‌خوای پیش بینی کنی بهش می‌گن متغیر وابسته و متغیری که ازش برای پیش بینی استفاده می‌کنی می‌گن متغیر مستقل.

این روش تحلیل سعی می‌کنه ضرایب یه معادله خطی رو پیدا کنه که با داشتن یک یا چند متغیر مستقل، بهترین پیش بینی رو برای مقدار متغیر وابسته به دست بیاره. رگرسیون خطی یه خط مستقیم یا سطحی رو پیدا می‌کنه که اختلاف بین مقادیر پیش بینی شده و واقعی رو به حداقل برسونه. ماشین حساب‌های ساده رگرسیون خطی از روش "کمترین مربعات" برای پیدا کردن بهترین خط برای داده‌های دو تایی استفاده می‌کنن. بعدش می‌تونی مقدار X (متغیر وابسته) رو از Y (متغیر مستقل) تخمین بزنی.

حالا بذار با یه مثال مفهوم رگرسیون خطی و کاربردش رو برات ساده‌تر کنم؛

فرض کن تو یه بستنی فروشی داری و می‌خوای بدونی تو روزای گرم چندتا بستنی می‌فروشی. مثلا اگه دما ۳۰ درجه باشه، چندتا بستنی فروش داری؟ اینجاست که رگرسیون خطی به کارت میاد.

فرض کن چند روز گذشته دمای هوا و تعداد بستنی هایی که فروختی رو یادداشت کردی. مثلا داده هات این جوریه:

• روز اول: دما ۲۰ درجه، فروش ۵۰ بستنی
• روز دوم: دما ۲۵ درجه، فروش ۷۰ بستنی
• روز سوم: دما ۳۰ درجه، فروش ۱۰۰ بستنی
• روز چهارم: دما ۳۵ درجه، فروش ۱۳۰ بستنی

حالا می‌خوای ببینی اگه دما ۲۸ درجه باشه، چندتا بستنی می‌تونی بفروشی. اینجاست که رگرسیون خطی میاد وسط و بهت کمک می‌کنه یه خط راست پیدا کنی که بهترین رابطه بین دما و فروش بستنی رو نشون بده.

چطوری کار می‌کنه؟

رگرسیون خطی یه خط صاف پیدا می‌کنه که بهترین توضیح دهنده رابطه بین دما (متغیر مستقل) و فروش بستنی (متغیر وابسته) باشه. فرمول این خط به شکل زیره:

y=mx+by = mx + by=mx+b

• yyy: تعداد بستنی هایی که می‌فروشی
• xxx: دمای هوا
• mmm: شیب خط، که نشون می‌ده با هر درجه افزایش دما، چندتا بستنی بیشتر می‌فروشی
• bbb: عرض از مبدا، که نشون می‌ده وقتی دما صفره، چندتا بستنی می‌فروشی (البته اینجا مفهومش کمتر مهمه)

چطوری ازش استفاده کنیم؟

با استفاده از داده هایی که داری، می‌تونی ضرایب mmm و bbb رو حساب کنی. مثلا فرض کن محاسبات نشون بده:

y=4x+10y = 4x + 10y=4x+10

این یعنی برای هر درجه افزایش دما، ۴ تا بستنی بیشتر می‌فروشی و وقتی دما صفره، ۱۰ تا بستنی می‌فروشی. حالا اگه بخوای بدونی تو دمای ۲۸ درجه چندتا بستنی می‌فروشی، فقط کافیه دما رو بذاری تو فرمول:

y=4(28)+10=112+10=122y = 4(28) + 10 = 112 + 10 = 122y=4(28)+10=112+10=122

پس تو دمای ۲۸ درجه، احتمالاً ۱۲۲ تا بستنی می‌فروشی.

رگرسیون خطی کمک می‌کنه تا بتونی بر اساس داده‌های گذشته، پیش بینی کنی که در شرایط مختلف چه اتفاقی می‌افته. این روش تو خیلی از زمینه‌ها مثل فروش، پزشکی، اقتصاد و حتی علوم اجتماعی کاربرد داره. با استفاده از این روش، می‌تونی تصمیم‌های بهتری بگیری و بهتر برنامه ریزی کنی.

چرا رگرسیون خطی مهمه؟

مدل‌های رگرسیون خطی نسبتا ساده ان و یه فرمول ریاضی قابل فهم بهت می‌دن که می‌تونه پیش بینی هایی انجام بده. این روش تو خیلی از زمینه‌ها مثل علوم زیستی، رفتاری، محیطی، اجتماعی و کسب وکار کاربرد داره. مدل‌های رگرسیون خطی یه روش اثبات شده برای پیش بینی علمی و قابل اعتماد آینده هستن. از اونجایی که این روش یه روش آماری قدیمیه، ویژگی‌های مدل‌های رگرسیون خطی خوب درک شدن و می‌تونن خیلی سریع آموزش ببینن.

استفاده از رگرسیون خطی توی کسب وکار

رگرسیون خطی به رهبران کسب وکار و سازمان‌ها کمک می‌کنه تصمیمات بهتری بگیرن. سازمان‌ها حجم زیادی از داده‌ها رو جمع آوری می‌کنن و رگرسیون خطی بهشون کمک می‌کنه از این داده‌ها برای مدیریت بهتر واقعیت استفاده کنن، به جای اینکه به تجربه و حدس تکیه کنن. می‌تونی حجم زیادی از داده‌های خام رو بگیری و تبدیل به اطلاعات کاربردی کنی.

همچنین می‌تونی از رگرسیون خطی برای فهم بهتر الگوها و روابطی که همکارانت تو کسب وکارتون قبلا دیده و فکر می‌کردن می‌دونن، استفاده کنی. مثلا، تحلیل داده‌های فروش و خرید می‌تونه بهت کمک کنه الگوهای خرید خاص تو روزها یا زمان‌های مشخص رو کشف کنی. اطلاعاتی که از تحلیل رگرسیون به دست میاد، می‌تونه به رهبران کسب وکار کمک کنه زمان هایی که محصولات شرکتشون تقاضای بالایی دارن رو پیش بینی کنن.

کاربردهای رگرسیون خطی

رگرسیون خطی یکی از اون ابزارهایی هست که وقتی بفهمی چطوری کار می‌کنه، می‌تونی ازش تو خیلی از زمینه‌ها استفاده کنی. بیایید با هم چند تا از کاربردهای جذابش رو بررسی کنیم.

۱. ارزیابی روندها و تخمین فروش

فرض کن می‌خوای پیش بینی کنی یه فروشنده در طول یک سال چقدر فروش داره. با استفاده از رگرسیون خطی می‌تونی متغیرهای مختلفی مثل سن، تحصیلات و سال‌های تجربه رو در نظر بگیری و ببینی که هر کدوم چقدر روی فروش تاثیر دارن. اینجوری می‌تونی بفهمی که چه عواملی باعث افزایش فروش می‌شن.

۲. تحلیل رفتار مشتری

رگرسیون خطی می‌تونه کمک کنه بفهمی که چه عواملی باعث می‌شه مشتری‌ها بیشتر خرید کنن. مثلاً اگه یه رستوران داری، می‌تونی تحلیل کنی که تبلیغات تلویزیونی، تخفیف‌ها یا حتی روزهای خاص هفته چقدر روی تعداد مشتری‌ها تأثیر داره.

مثال:
فرض کن داده‌های شما اینجوری باشه:

• روزهای عادی: ۵۰ مشتری
• روزهای تخفیف: ۱۰۰ مشتری
• روزهای تبلیغات: ۸۰ مشتری

با استفاده از رگرسیون خطی، می‌تونی بفهمی که ترکیب این عوامل چطور روی تعداد مشتری‌ها تأثیر می‌ذاره.

3. تحلیل کشش قیمت

وقتی قیمت یه محصول تغییر می‌کنه، معمولاً رفتار مصرف کننده‌ها هم تغییر می‌کنه. رگرسیون خطی می‌تونه کمک کنه بفهمی که این تغییرات قیمت چقدر روی مصرف تاثیر می‌ذاره. مثلاً اگه قیمت یه محصول خاص مدام تغییر کنه، با رگرسیون می‌تونی ببینی که آیا مصرف کم می‌شه یا نه. اگه مصرف به طور چشمگیری کم نشه، می‌تونی بفهمی تا چه قیمتی مردم حاضرن اون محصول رو بخرن. این اطلاعات برای مدیران فروشگاه‌ها خیلی مفیده.

4. بهینه سازی تبلیغات

شرکت‌های بزرگ مثل گوگل و فیسبوک از رگرسیون خطی برای بهینه سازی تبلیغات استفاده می‌کنن. اونا با تحلیل داده‌های گذشته می‌تونن بفهمن که چه نوع تبلیغاتی در چه زمانی بیشترین تأثیر رو داره.

مثال:
اگه داده‌های تبلیغاتی شما نشون بده که تبلیغات صبحگاهی بهتر از تبلیغات عصرگاهی جواب می‌ده، می‌تونی بودجه تبلیغاتیت رو بیشتر روی صبح‌ها متمرکز کنی.

5. پیش بینی روند بازار

رگرسیون خطی توی حوزه‌های مالی و بورس هم خیلی کاربرد داره. سرمایه گذارا از این روش استفاده می‌کنن تا روند قیمت سهام و اوراق بهادار رو پیش بینی کنن و تصمیمات بهتری بگیرن.

6. تحلیل‌های پزشکی

در زمینه پزشکی، رگرسیون خطی می‌تونه برای پیش بینی روند بیماری‌ها و تأثیر درمان‌ها استفاده بشه. مثلاً می‌شه رابطه بین دوز دارو و کاهش علائم بیماری رو بررسی کرد.

7. ارزیابی ریسک در شرکت بیمه

رگرسیون خطی توی تحلیل ریسک هم خیلی کاربرد داره. مثلاً یه شرکت بیمه می‌تونه از این روش برای تحلیل و برآورد هزینه‌های خسارت بیمه نامه‌های مختلف استفاده کنه. با این تحلیل، مدیران شرکت می‌تونن تصمیم بگیرن که کجاها ریسک بیشتری بپذیرن و کجاها محتاط‌تر باشن.

8. تحلیل ورزشی

رگرسیون خطی فقط برای کسب وکار نیست؛ توی ورزش هم خیلی کاربرد داره. مثلاً ممکنه بخوای بدونی که تعداد بازی‌های برده یه تیم بسکتبال در فصل، به تعداد امتیازاتی که در هر بازی می‌گیرن مربوطه یا نه. با رگرسیون خطی می‌تونی این رابطه رو تحلیل کنی. همچنین می‌تونی ببینی که آیا تعداد بازی‌های برده با میانگین امتیازاتی که حریف هاشون می‌گیرن رابطه داره یا نه. با یه مدل خوب، می‌تونی پیش بینی کنی که یه تیم چقدر احتمال بردن بازی‌ها رو داره.

رگرسیون خطی یه ابزار قدرتمند و ساده ست که می‌تونه توی خیلی از زمینه‌ها بهت کمک کنه. از پیش بینی فروش گرفته تا تحلیل رفتار مشتری و حتی پیش بینی روند بازار و تحلیل‌های پزشکی، این روش همیشه یه راهکار خوب ارائه می‌ده. با یادگیری و استفاده از رگرسیون خطی، می‌تونی تصمیمات بهتری بگیری و کسب وکار یا تحقیقاتت رو بهبود بدی.

فرضیات کلیدی برای رگرسیون خطی موثر

برای اینکه بتونی یه تحلیل رگرسیون خطی موفق داشته باشی، باید چندتا فرضیه رو در نظر بگیری:

برای هر متغیر:

• تعداد موارد معتبر، میانگین و انحراف معیارشون رو در نظر بگیر.

برای هر مدل:

• ضرایب رگرسیون، ماتریس همبستگی، همبستگی جزئی و کلی، مقدار RRR، R2R^2R2، R2R^2R2 تعدیل شده، تغییر در R2R^2R2، خطای استاندارد برآورد، جدول تحلیل واریانس، مقادیر پیش بینی شده و باقیمانده‌ها رو بررسی کن.
• همینطور، بازه‌های اطمینان ۹۵ درصدی برای هر ضریب رگرسیون، ماتریس واریانس-کوواریانس، ضریب تورم واریانس، تحمل، آزمون دوربین-واتسون، مقادیر فاصله ای (ماهانلوبیس، کوک و مقادیر نفوذ)، DfBeta، DfFit، بازه‌های پیش بینی و اطلاعات تشخیصی موردی رو هم در نظر بگیر.

نمودارها:

• به نمودارهای پراکندگی، نمودارهای جزئی، هیستوگرام‌ها و نمودارهای احتمال نرمال نگاه کن.

داده ها:

• متغیرهای وابسته و مستقل باید کمی باشن. متغیرهای دسته ای مثل دین، رشته تحصیلی یا محل سکونت باید به متغیرهای دودویی (dummy) یا انواع دیگه ای از متغیرهای کنتراست تبدیل بشن.

فرضیات دیگه:

• برای هر مقدار از متغیر مستقل، توزیع متغیر وابسته باید نرمال باشه.
• واریانس توزیع متغیر وابسته باید برای همه مقادیر متغیر مستقل ثابت باشه.
• رابطه بین متغیر وابسته و هر متغیر مستقل باید خطی باشه و همه مشاهدات باید مستقل باشن.

مطمئن شو که داده هات به فرضیات رگرسیون خطی می‌خورن

قبل از اینکه بخوای رگرسیون خطی رو انجام بدی، باید مطمئن شی که داده هات قابل تحلیل با این روش هستن. داده هات باید از چندتا فرضیه رد بشن.

چطور این فرضیات رو بررسی کنیم:

• متغیرها باید پیوسته باشن: مثلاً زمان، فروش، وزن و نمرات آزمون.
• از نمودار پراکندگی استفاده کن: سریعاً بفهمی که آیا بین این دو متغیر رابطه خطی وجود داره یا نه.
• مشاهدات باید مستقل باشن: یعنی هیچ وابستگی بین مشاهدات نباشه.
• داده هات نباید دارای موارد خارج از محدوده باشن: مواردی که خیلی از بقیه داده‌ها فاصله دارن.
• بررسی همسانی واریانس ها: یعنی اینکه واریانس‌ها (پراکنده بودن داده ها) در طول خط رگرسیون مشابه باشن.
• باقیمانده‌های خط رگرسیون باید توزیع نرمال داشته باشن.

این موارد رو بررسی کنی، می‌تونی مطمئن بشی که داده هات برای رگرسیون خطی مناسب هستن و تحلیل دقیق‌تری داشته باشی.

مزایای کلیدی رگرسیون خطی

رگرسیون خطی یه ابزار آماری محبوب توی داده کاوی و علوم داده ست و دلایل خوبی هم برا این محبوبیت داره. بیایید با هم چند تا از مزایای اصلیش رو بررسی کنیم.

۱. پیاده سازی آسون

رگرسیون خطی از نظر محاسباتی خیلی ساده ست و نیاز به کارهای پیچیده و اضافه قبل یا بعد از راه اندازی مدل نداره. یعنی می‌تونی با کمترین دردسر ازش استفاده کنی و نگهداریش هم آسونه.

۲. قابل فهم بودن

برخلاف مدل‌های پیچیده‌تر مثل شبکه‌های عصبی، رگرسیون خطی خیلی سر راست و قابل فهمه. این یعنی می‌تونی به راحتی بفهمی کدوم متغیر ورودی باعث تغییر توی متغیر خروجی می‌شه، چیزی که توی مدل‌های پیچیده‌تر مثل یه جعبه سیاهه.

۳. مقیاس پذیری

رگرسیون خطی از نظر محاسباتی سبک وزنه، پس برای مواقعی که مقیاس بندی مهمه، خیلی خوب جواب می‌ده. مثلا وقتی که حجم داده‌ها زیاد می‌شه (کلان داده ها)، این مدل همچنان کارایی خوبی داره.

۴. مناسب برای محیط‌های آنلاین

از اونجایی که محاسبات رگرسیون خطی خیلی راحته، می‌تونی ازش تو محیط‌های آنلاین هم استفاده کنی. این مدل می‌تونه با هر مثال جدید آموزش ببینه و در زمان واقعی پیش بینی کنه. برخلاف شبکه‌های عصبی یا ماشین‌های بردار پشتیبان که محاسبات سنگین و زمان زیادی برای بازآموزی نیاز دارن، رگرسیون خطی سریع و مقرون به صرفه ست و برای کاربردهای آنلاین خیلی مناسبه.

این ویژگی‌ها نشون می‌ده که چرا رگرسیون خطی یه مدل محبوب برای حل مسائل دنیای واقعی توی یادگیری ماشین و علوم داده ست.

معادله رگرسیون خطی

بذار یه مثال بزنیم تا بهتر بفهمیم. فرض کن یه دیتاست داریم که اندازه RAM و هزینه شون رو پوشش می‌ده.

تو این مثال، دیتاست دو ویژگی داره: حافظه (ظرفیت) و هزینه. هر چی RAM بیشتر باشه، هزینه خریدش هم بیشتر می‌شه.

اگه RAM رو روی محور X و هزینه ش رو روی محور Y بذاریم، یه خط از گوشه پایین چپ نمودار به گوشه بالا راست می‌کشه که رابطه بین X و Y رو نشون می‌ده. اگه این داده‌ها رو روی نمودار پراکندگی رسم کنیم، همچین نموداری می‌گیریم:

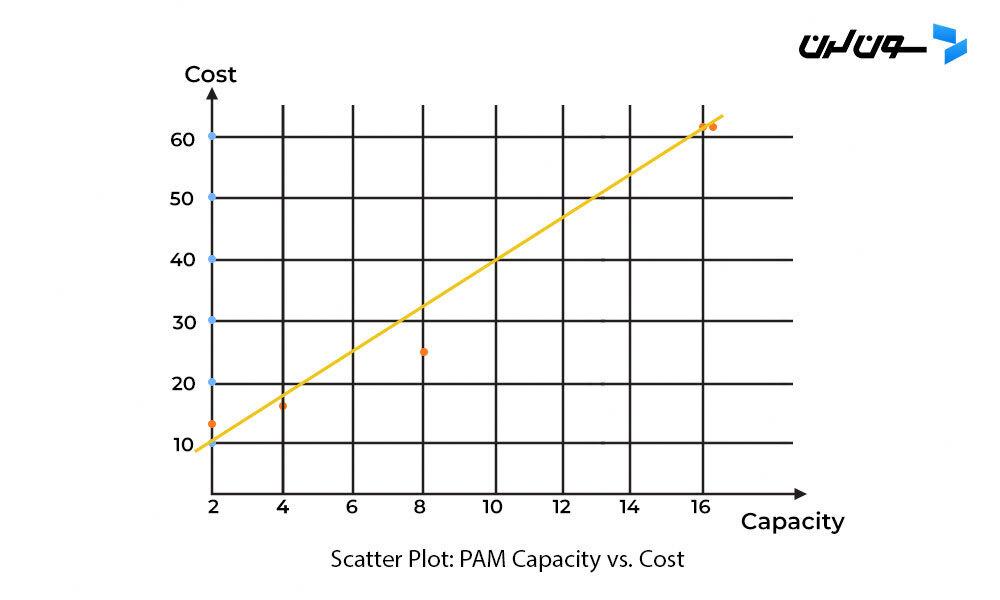
حالا نسبت حافظه به هزینه ممکنه بسته به تولیدکننده‌ها و نسخه‌های مختلف RAM متفاوت باشه، ولی روند داده‌ها یه الگو رو نشون می‌ده. داده‌های گوشه پایین چپ نمودار RAM‌های ارزون‌تر با حافظه کمتر رو نشون می‌ده و خط ادامه پیدا می‌کنه تا گوشه بالا راست نمودار که RAM‌های با ظرفیت بالاتر و هزینه بیشتر قرار دارن.

مدل رگرسیون یه تابع خطی بین متغیرهای X و Y تعریف می‌کنه که بهترین نمایش دهنده رابطه بین این دو باشه. این تابع همون خط مورب تو نموداره که هدفش پیدا کردن یه "خط رگرسیون" بهینه ست که بهترین تناسب رو با همه نقاط داده داشته باشه.

از نظر ریاضی، این خطوط مورب از این معادله پیروی می‌کنند:

Y=mX+bY = mX + bY=mX+b

• XXX: متغیر وابسته (هدف)
• YYY: متغیر مستقل
• mmm: شیب خط (شیب به صورت "صعود" نسبت به "پیشرفت" تعریف می‌شه)

اما متخصصان یادگیری ماشین یه نشانه گذاری متفاوت دارن:

y(x)=p0+p1∗xy(x) = p0 + p1 * xy(x)=p0+p1∗x

که در اینجا:

• yyy: متغیر خروجی. متغیر yyy مقداری پیوسته ست که مدل سعی در پیش بینی اون داره.
• xxx: متغیر ورودی. توی یادگیری ماشین، xxx به ویژگی‌ها اشاره داره، در حالی که در آمار به عنوان متغیر مستقل شناخته می‌شه. متغیر xxx اطلاعات ورودی ای رو که به مدل در هر لحظه داده می‌شه، نشون می‌ده.
• p0p0p0: نقطه تقاطع با محور yyy (یا همون بایاس).
• p1p1p1: ضریب رگرسیون یا ضریب مقیاس. توی آمار کلاسیک، p1p1p1 معادل شیب خط بهترین تناسب در مدل رگرسیون خطیه.
• pipipi: وزن‌ها (به طور کلی).

بنابراین، مدل سازی رگرسیون همه اش درباره پیدا کردن مقادیر پارامترهای نامعلوم معادله ست، یعنی مقادیر p0p0p0 و p1p1p1 (وزن ها).

معادله برای رگرسیون خطی چندگانه

این فرآیند برای رگرسیون خطی ساده که یه ویژگی یا متغیر مستقل داره، به کار می‌ره. اما می‌شه مدل رگرسیون رو برای چندین ویژگی هم استفاده کرد و معادله رو برای تعداد متغیرهای موجود در دیتاست گسترش داد.

معادله برای رگرسیون خطی چندگانه مشابه معادله برای رگرسیون خطی ساده ست، یعنی:

y(x)=p0+p1x1y(x) = p0 + p1x1y(x)=p0+p1x1

به اضافه وزن‌ها و ورودی‌های دیگه برای ویژگی‌های مختلف که به صورت p(n)x(n)p(n)x(n)p(n)x(n) نمایش داده می‌شه. فرمول برای رگرسیون خطی چندگانه به این شکل خواهد بود:

y(x)=p0+p1x1+p2x2+…+p(n)x(n)y(x) = p0 + p1x1 + p2x2 + \ldots + p(n)x(n)y(x)=p0+p1x1+p2x2+…+p(n)x(n)

مدل یادگیری ماشین از این فرمول و مقادیر وزن‌های مختلف برای رسم خطوطی که به بهترین شکل با داده‌ها منطبق می‌شن، استفاده می‌کنه.

علاوه بر تابع پیش بینی، مدل رگرسیون از یه تابع هزینه هم استفاده می‌کنه تا وزن‌ها رو بهینه کنه. تابع هزینه در رگرسیون خطی به صورت خطای میانگین مربعات (MSE) یا خطای میانگین مربعات ریشه ای تعریف می‌شه.

اساساً، MSE تفاوت میانگین مربعات بین مقادیر واقعی و پیش بینی شده ی مشاهدات رو اندازه گیری می‌کنه. خروجی تابع هزینه یا امتیاز مرتبط با مجموعه وزن‌های فعلی ست و معمولاً یه عدد واحده. هدف اینجا کاهش MSE برای افزایش دقت مدل رگرسیونه.

ریاضی

با داشتن معادله ساده خطی y=mx+by = mx + by=mx+b، می‌تونیم مقادیر MSE رو محاسبه کنیم:

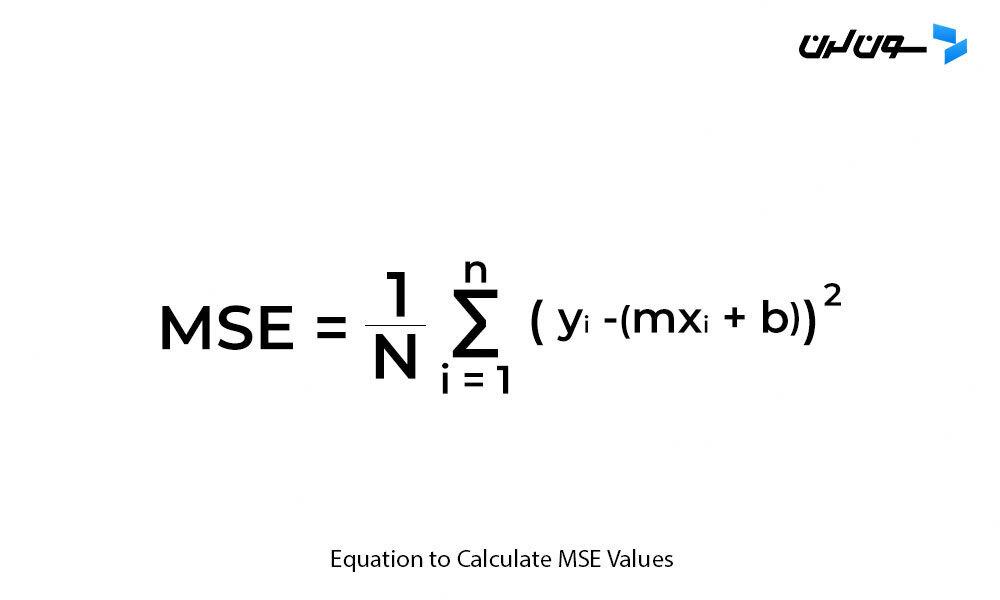
که در اینجا:

• NNN: تعداد کل مشاهدات (نقاط داده)
• 1N∑i=1N\frac{1}{N} \sum_{i=1}^{N}N1​∑i=1N​: میانگین
• yiy_iyi​: مقدار واقعی یه مشاهده
• mxi+bmx_i + bmxi​+b: پیش بینی

علاوه بر تابع هزینه، از الگوریتم "Gradient Descent" هم برای کاهش MSE و پیدا کردن خط بهترین تناسب برای یه مجموعه داده آموزشی استفاده می‌شه، و این باعث بهبود کلی کارایی مدل رگرسیون می‌شه.

معادله برای رگرسیون خطی می‌تونه به این صورت تصویرسازی بشه:

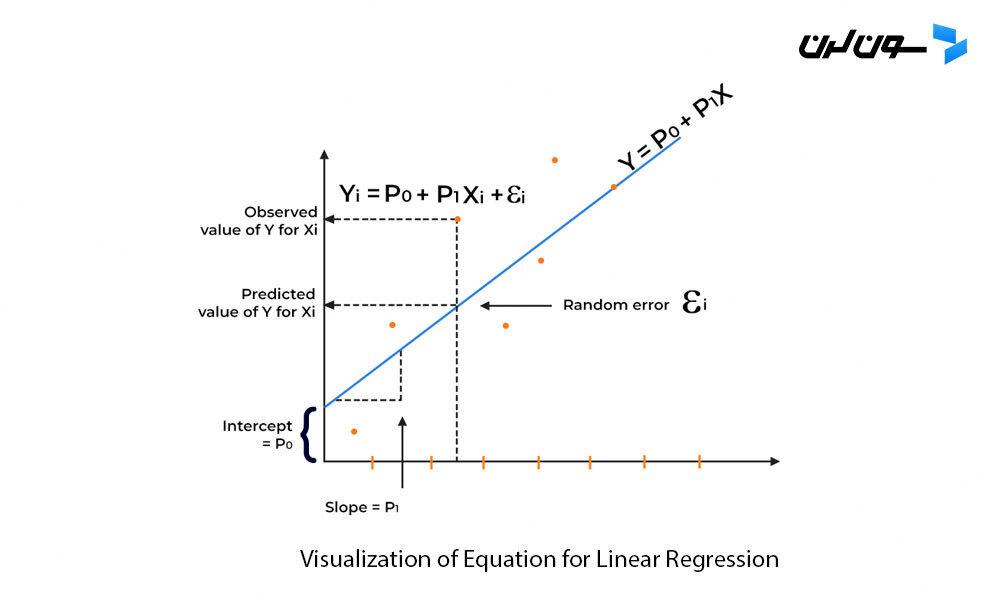
انواع رگرسیون خطی با مثال

رگرسیون خطی یکی از پایه‌های اصلی در بسیاری از کاربردهای هوش مصنوعی و داده کاویه. این تکنیک آماری به کسب وکارها کمک می‌کنه تا روندها رو ارزیابی کنن و پیش بینی‌های دقیقی انجام بدن. بیایید با هم انواع مختلف رگرسیون خطی رو بررسی کنیم.

۱. رگرسیون خطی ساده

رگرسیون خطی ساده رابطه بین یک متغیر وابسته (ورودی) و یک متغیر مستقل (خروجی) رو نشون می‌ده. این نوع رگرسیون بیشتر برای بررسی این موارد استفاده می‌شه:

• قدرت رابطه بین دو متغیر:
  مثال: رابطه بین سطح آلودگی هوا و دمای بالا.
• ارزش متغیر وابسته بر اساس متغیر مستقل:
  مثال: سطح آلودگی هوا در یک دمای خاص.

۲. رگرسیون خطی چندگانه

رگرسیون خطی چندگانه رابطه بین دو یا چند متغیر مستقل و یک متغیر وابسته رو مشخص می‌کنه. این نوع رگرسیون به پیش بینی روندها و تعیین ارزش‌های آینده کمک می‌کنه.

مثال: برای محاسبه فشار خون، می‌تونیم قد، وزن و میزان ورزش رو به عنوان متغیرهای مستقل در نظر بگیریم و با استفاده از رگرسیون خطی چندگانه رابطه بین این سه متغیر مستقل و فشار خون رو تحلیل کنیم.

۳. رگرسیون لجستیک

رگرسیون لجستیک (یا مدل لجستیک) زمانی استفاده می‌شه که یک متغیر وابسته و چندین متغیر مستقل داریم. تفاوت اصلی بین رگرسیون چندگانه و لجستیک اینه که در رگرسیون لجستیک، متغیر وابسته مقداری گسسته (باینری یا مرتبه ای) داره.

مثال: احتمال قبول یک پیشنهاد روی وب سایت شما (متغیر وابسته) رو می‌تونیم با ویژگی‌های مختلف بازدیدکنندگان مثل سایت هایی که از اونجا اومدن، تعداد بازدیدها و فعالیت هایشون روی سایت (متغیرهای مستقل) بررسی کنیم. این کار به شما کمک می‌کنه تصمیم بگیرید که آیا پیشنهاد رو تبلیغ کنید یا نه.

۴. رگرسیون ترتیبی

رگرسیون ترتیبی شامل یک متغیر وابسته دوگانه و یک متغیر مستقله که می‌تونه ترتیبی یا اسمی باشه. این روش به تعامل بین متغیرهای وابسته با سطوح مرتب و یک یا چند متغیر مستقل کمک می‌کنه.

مثال: در یک نظرسنجی که پاسخ دهندگان باید به سوالات با گزینه‌های "موافق" یا "مخالف" پاسخ بدن، می‌تونیم سطوح بیشتری مثل "کاملاً موافق"، "موافق"، "مخالف" و "کاملاً مخالف" اضافه کنیم تا ترتیب طبیعی در پاسخ‌ها رو ببینیم. رگرسیون ترتیبی به پیش بینی متغیر وابسته با دسته‌های مرتب کمک می‌کنه.

۵. رگرسیون لجستیک چندگانه

رگرسیون لجستیک چندگانه زمانی استفاده می‌شه که متغیر وابسته اسمی و دارای بیش از دو سطح باشه. این روش رابطه بین یک متغیر وابسته اسمی و یک یا چند متغیر مستقل پیوسته رو مشخص می‌کنه.

مثال: انتخاب برنامه تحصیلی توسط دانش آموزان مدرسه رو می‌تونیم با استفاده از این روش مدل سازی کنیم. برنامه‌های تحصیلی می‌تونن شامل برنامه‌های فنی، ورزشی و آکادمیک باشن. با در نظر گرفتن ویژگی هایی مثل توانایی خواندن و نوشتن دانش آموزان، جنسیت و جوایز دریافتی، می‌تونیم نوع برنامه تحصیلی انتخابی رو پیش بینی کنیم.

در اینجا، متغیر وابسته انتخاب برنامه‌های تحصیلی با سطوح مختلف (نامرتب) است. تکنیک رگرسیون لجستیک چندگانه برای پیش بینی در چنین مواردی استفاده می‌شه.

سوالات متداول

1. رگرسیون خطی چیه؟

رگرسیون خطی یه روش آماریه که برای مدل سازی رابطه بین یه متغیر وابسته و یک یا چند متغیر مستقل استفاده می‌شه. این روش به ما کمک می‌کنه تا پیش بینی‌های دقیقی انجام بدیم.

2. کی باید از رگرسیون خطی استفاده کنیم؟

وقتی بخوایم رابطه خطی بین متغیرها رو بررسی کنیم و ازش برای پیش بینی استفاده کنیم، رگرسیون خطی بهترین گزینه ست. این روش توی تحلیل‌های مالی، پزشکی، صنعتی و خیلی از حوزه‌های دیگه کاربرد داره.

3. محدودیت‌های رگرسیون خطی چیه؟

محدودیت‌های رگرسیون خطی شامل اینه که فرض می‌کنه رابطه بین متغیرها خطیه، به داده‌های خارج از محدوده حساسه و برای تعداد زیادی متغیرها مناسب نیست. این روش برای روابط پیچیده و غیرخطی خیلی مناسب نیست.

4. چطور می‌شه دقت مدل رگرسیون خطی رو بالا برد؟

برای افزایش دقت مدل رگرسیون خطی می‌تونی از تبدیلات ریاضی، حذف داده‌های خارج از محدوده و استفاده از رگرسیون چندگانه استفاده کنی. این کارها به بهبود دقت مدل کمک می‌کنه.

5. تفاوت بین رگرسیون خطی ساده و رگرسیون خطی چندگانه چیه؟

رگرسیون خطی ساده فقط یه متغیر مستقل داره، ولی رگرسیون خطی چندگانه چند تا متغیر مستقل داره. رگرسیون چندگانه برای مدل سازی روابط پیچیده‌تر استفاده می‌شه.

جمع بندی

همون طور که متوجه شدید، مدل‌های رگرسیون خطی بر اساس یک فرمول ریاضی ساده و قابل فهم هستن که به ما کمک می‌کنن پیش بینی‌های دقیقی انجام بدیم. این مدل‌ها توی حوزه‌های مختلف کسب وکار و رشته‌های علمی مثل علوم اجتماعی، مدیریت، محیط زیست و علوم کامپیوتر کاربرد دارن.

رگرسیون خطی با پایه علمی خودش، تونسته به طور قابل اعتمادی روندهای آینده رو پیش بینی کنه. این مدل‌ها به خاطر سادگی و قابلیت فهمیدن راحت، خیلی سریع آموزش داده می‌شن و به همین دلیل به طور گسترده ای استفاده می‌شن.

آیا این مقاله بهت کمک کرد تا رگرسیون خطی رو بهتر بفهمی؟ نظر تو برامون مهمه! زیر همین مطلب کامنت بذار. خوشحال می‌شیم ازت بشنویم!